前言
上次打NISCCTF2019留下来的一道题,关于pyc文件逆向,接着这道题把Python Bytecode解混淆相关的知识和工具全部过一遍。同时在已有的基础上进一步创新得到自己的成果,这是下篇,更近一步进行还原混淆过的pyc文件。
图表示法
目前可以见到最多的解混淆或者去花指令的手段类似于对于指令的匹配替换,甚至于可以说上一篇中的活跃代码分析也是带执行流分析的简单替换过程。但如果我想构建一个对于某种混淆方式的通用解法,只是工作于指令级别始终不够方便。那么需要一种新的方式去处理这些指令。
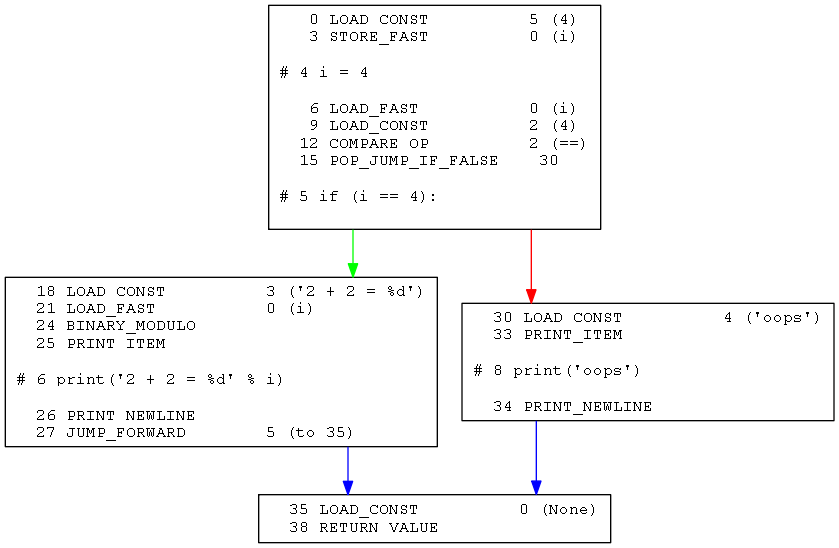
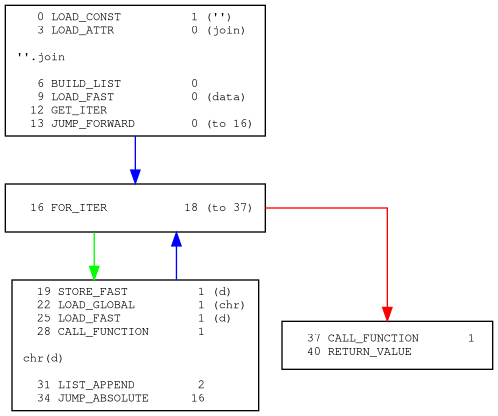
在这里选用一种基于有向图的表示法,也即在执行流跳转的位置进行分割,使指令之间成块,相互之间用箭头相关联。如下图:
有了这种表示法之后就可以方便的在独立的块之间进行遍历和处理。
Bytecode graph
这个工具来自这里,实现了基本的Python字节码到图表示的转换过程,但是相比起来功能较为单薄。
上一篇中把恶意指令全部NOP掉了,现在想把NOP指令用这个库全部去除,首先尝试调用API画出所有函数的图:
import bytecode_graph
from dis import opmap
import sys
import marshal
pyc_file = open(sys.argv[1], "rb").read()
pyc = marshal.loads(pyc_file[8:])
bcg = bytecode_graph.BytecodeGraph(pyc)
graph = bytecode_graph.Render(bcg, pyc).dot()
graph.write_png('example_graph.png')
结果崩溃了:
Traceback (most recent call last):
File "./gen_graph.py", line 9, in <module>
graph = bytecode_graph.Render(bcg, pyc).dot()
File "/tmp/flare-bytecode_graph/bytecode_gra/render.py", line 112, in dot
lbl = disassemble(self.co, start=start.addr, stop=stop.addr+1,
AttributeError: 'NoneType' object has no attribute 'addr'
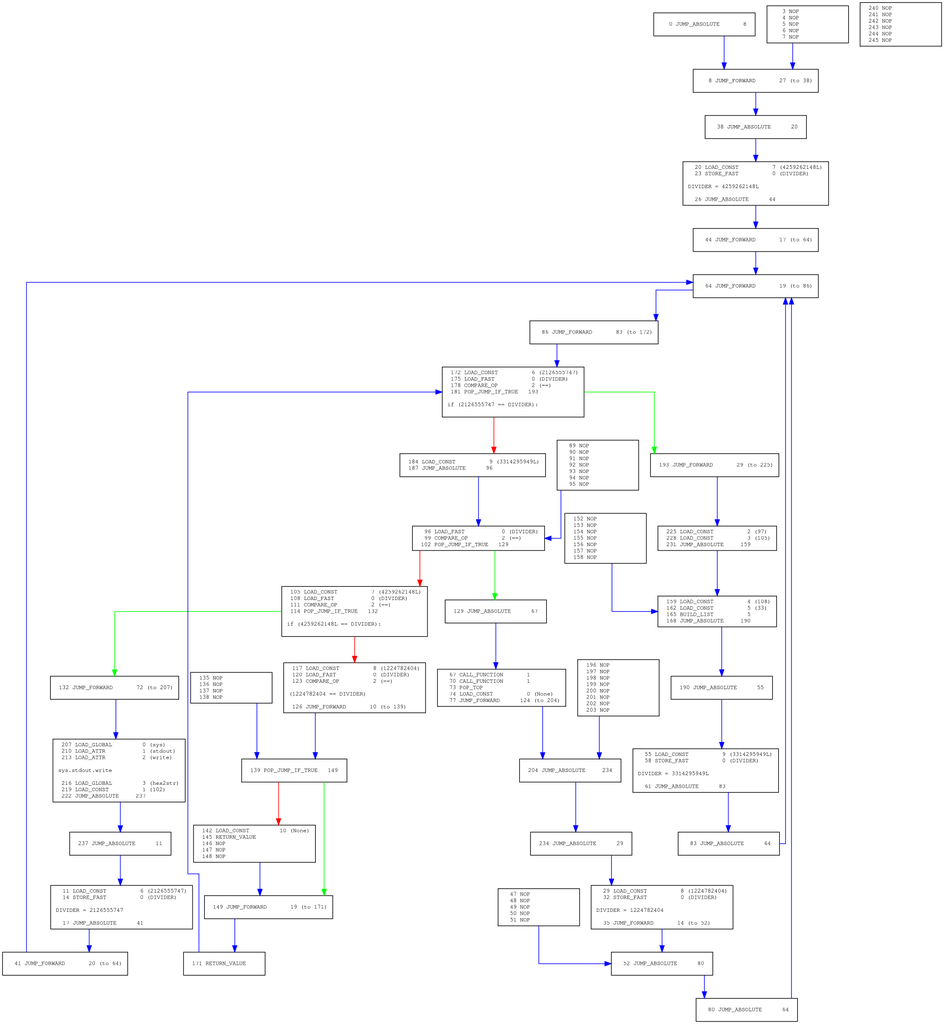
查看源码发现是渲染模块里获取block的函数写的时候没有考虑到一个corner case,修复之后成功生成图像:
首先观察执行流可以很明显的看出是进行过控制流扁平化处理的,然后尝试阅读文档去除多余的NOP分支。
去除NOP的代码:
def remove_nop_inner(co):
bcg = bytecode_graph.BytecodeGraph(co)
nodes = [x for x in bcg.nodes()]
for n in nodes:
if n.opcode == NOP:
bcg.delete_node(n)
return bcg.get_code()
def remove_nop(co):
#co = remove_nop_inner(co)
inner = list()
for i in range(len(co.co_consts)):
if hasattr(co.co_consts[i], 'co_code'):
inner.append(remove_nop_inner(co.co_consts[i]))
else:
inner.append(co.co_consts[i])
co.co_consts = tuple(inner)
return co
再次运行然后再次崩溃:
Traceback (most recent call last):
File "./de.py", line 163, in <module>
mode = remove_nop(mode)
File "./de.py", line 108, in remove_nop
inner.append(remove_nop_inner(co.co_consts[i]))
File "./de.py", line 100, in remove_nop_inner
return bcg.get_code()
File "/home/fx-ti/ctf/nisc2019/py/deconfus/flare-bytecode_graph/bytecode_gra/bytecode_graph.py", line 225, in get_code
new_co_lineno = self.calc_lnotab()
File "/home/fx-ti/ctf/nisc2019/py/deconfus/flare-bytecode_graph/bytecode_gra/bytecode_graph.py", line 173, in calc_lnotab
new_offset = current.co_lnotab - prev_lineno
TypeError: unsupported operand type(s) for -: 'NoneType' and 'int'
这个错误就很有意思了,和之后成功还原仍然不能使用uncompyle6得到源码有关。都是在对co_lnotab这个部分的解析中出现了错误导致的崩溃。
Python通过co_lnotab将字节码和源码行数对齐,服务于源码调试。co_lnotab中的数据两字节为一组,分别是字节码的增量偏移和源码的增量偏移。
>>> import marshal
>>> f = open('../../mo.pyc')
>>> f.read(8)
'x03xf3rnLiT\'
>>> c = marshal.load(f)
>>> list(map(ord,c.co_lnotab))
[12, 2, 9, 6, 9, 5, 9, 3, 9, 3, 9, 18, 37, 2, 18, 2]
也即都从0开始计算,首先字节码增加了12条指令,源码就到了第2行,这样不断递增得到的对应关系。
>>> dis.dis(c.co_code)
0 JUMP_ABSOLUTE 670
3 NOP
4 NOP
5 NOP
6 NOP
7 NOP
8 NOP
9 NOP
10 NOP
11 NOP
>> 12 LOAD_FAST 0 (0) # 源码第2行
15 COMPARE_OP 2 (==)
18 POP_JUMP_IF_TRUE 39
然而这样的对应关系在修改了指令成为NOP之后便没有意义,因为从带参数的指令变成不带参数的指令定然会导致字节码偏移计算出错。更何况这个样本的pyc文件有的函数的co_lnotab是残缺的,便会导致尝试解析它的过程失败。然而不巧这个库和uncompyle6都是会解析的。
但即使是这样,这款库作为图的生成器,自带的指令解析和引用解析都不错,仍旧写出图生成脚本予以采用。并对之前的补丁操作提出了pr。
import bytecode_gra as bytecode_graph
from dis import opmap
import sys
import marshal
pyc_file = open(sys.argv[1], "rb").read()
pyc = marshal.loads(pyc_file[8:])
for x in pyc.co_consts:
if hasattr(x, 'co_code'):
bcg = bytecode_graph.BytecodeGraph(x)
graph = bytecode_graph.Render(bcg, x).dot()
try:
graph.write_png(x.co_name + '.png')
except Exception, e:
print(e)
print(x.co_name)
bcg = bytecode_graph.BytecodeGraph(pyc)
graph = bytecode_graph.Render(bcg, pyc).dot()
graph.write_png('module.png')
Bytecode simplifier
这个比之前那个更加强大,来自于这篇博客。
这个简化器原本是为了针对PjOrion解混淆而开发的,说来也是有意思,我这个样本被命中了PjOrion v2的特征签名。
在分析上它同样使用遍历执行流的方式得到实际字节码并分离成一个一个基本块,特指只有一个入口和一个出口的一连串指令
可以看到完全无视之前生成的NOP。
在表示上直接使用networkx.DiGraph组织有向图,提供完整API,在类似if分支时正确分支为explicit属性的边,失败分支是implicit属性的边。正常的跳转的边都是explicit的。
自带的解混淆功能
Forwarder elimination
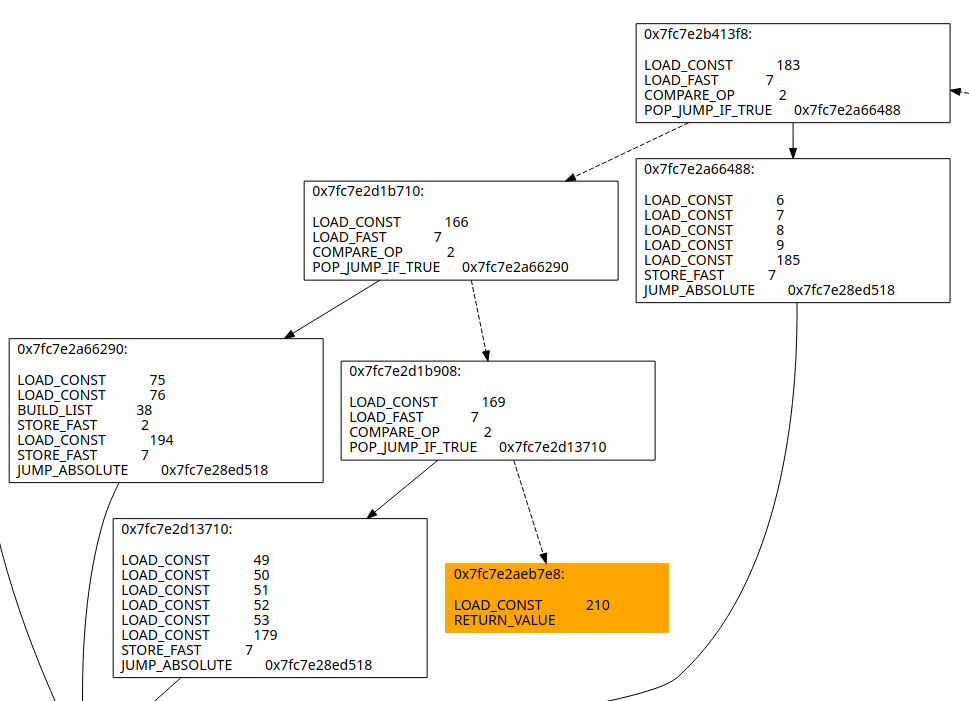
forwarder定义为只由一条跳转语句构成的基本块,只是转移了执行流没有任何有用操作。
黄色高亮的基本块就是一个forwarder,下图是去除以后。
Basic block merging
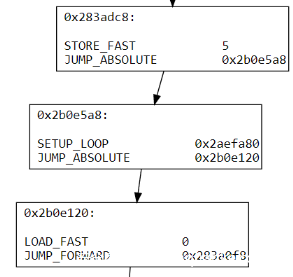
一个基本块可以被它的父基本块合并,当且仅当它只有这一个父基本块,且它的父基本块只有它一个子基本块。
高亮的基本块都能合并成为一个基本块,既然没有用,那么控制流转移指令被全部删除。
具体实现可以参考simplifier.py里的源码。
自己写的反控制流扁平化功能
首先还是在不添加简化流程的情况下运行,程序再次崩溃:
INFO:simplifier:43 basic blocks eliminated
Traceback (most recent call last):
File "./main.py", line 72, in <module>
process(args.ifile, args.ofile)
File "./main.py", line 58, in process
deob = parse_code_object(rootCodeObject)
File "./main.py", line 20, in parse_code_object
co_codestring = deobfuscate(codeObject.co_code)
File "/tmp/sim/deobfuscator.py", line 75, in deobfuscate
render_graph(simplifier.bb_graph, 'after_forwarder.svg')
File "/tmp/sim/utils/rendergraph.py", line 34, in render_graph
entryblock = nx.get_node_attributes(bb_graph, 'isEntry').keys()[0]
IndexError: list index out of range
分析之后发现是在forwarder elimination之后把有入口点属性的基本块给消除了。修改源码在修改之后传递属性即可,同样提交pr。
终于来到编写部分,在这里阐明控制流扁平化之后在本样本的特征:
- 入口点指定好第一个执行的块的常量然后进入分发基本块链
- 在分发基本块链中不断查找,只有在常量相等时进入正确分支执行对应基本块,否则进入失败分支继续查找
- 在实际执行基本块结尾指定下一块实际基本块的常量值
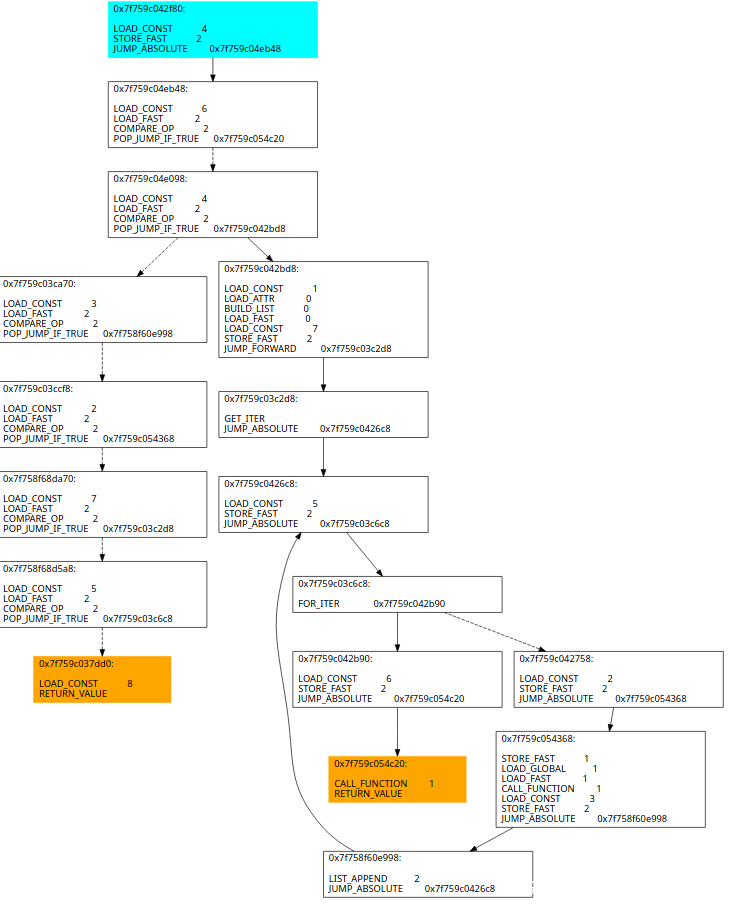
举例如下:
那么整个过程可以分成几步:
- 沿着分发基本块遍历得到分发关系,再找到实际基本块的尾端确认下一基本块的常量,之后配对得到实际关系
- 再修改配对的基本块之间的执行流,还原他们的先后执行次序
- 对入口点设置的常量的对应实际基本块设置成为入口点
- 把分发基本块链和入口点全部删除
- 把所有基本块尾部存在的设置常量的指令删除
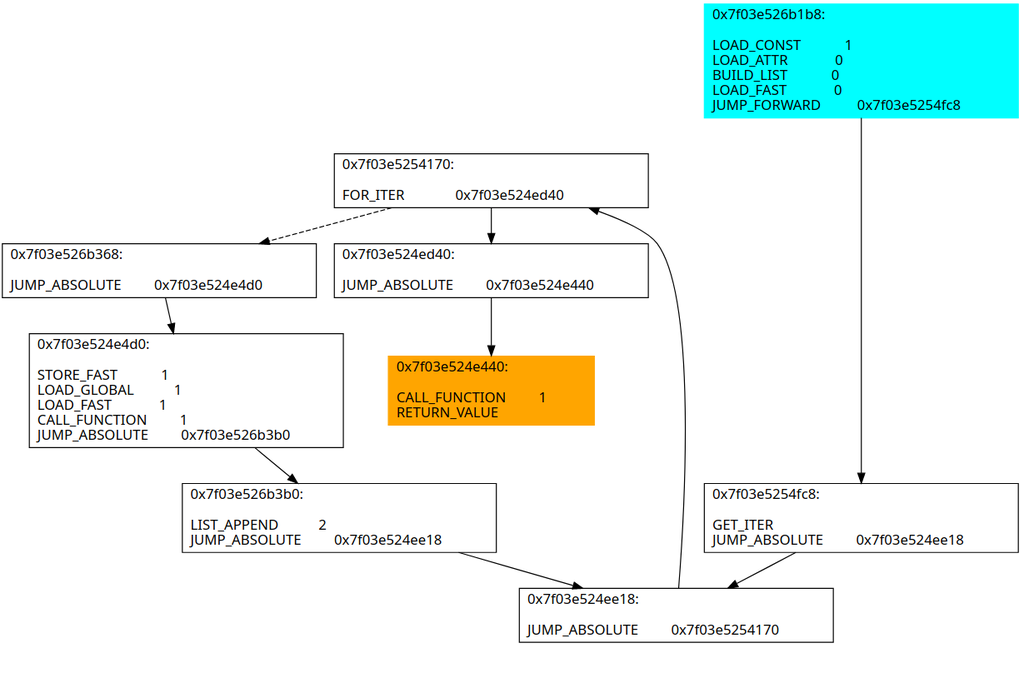
可以看到原来打乱的控制流还原了,但是基本块之间还是有些琐碎,怎么办呢?
很简单,再跑一次forwarder elimination和merge blocks就行了!
可以看到这样就已经还原到近似于CPython生成的字节码了。虽然因为之前说过的原因用不了uncompyle6,但是可以用unpyc进行反编译可以得到:
def str2hex(string):
#[NODE: 0]
ret = []
#[NODE: 19]
for char in string:
ret(ord(char))
#[NODE: 48]
return ret
def hex2str(data):
#[NODE: 19]
for d in data:
#[NODE: 37]
return [](data)
def p_s():
sys(hex2str([115L, 117L, 99L, 99L, 101L, 115L, 115L, 33L]))
def p_f():
sys(hex2str([102L, 97L, 105L, 108L, 33L]))
def count(data):
#[NODE: 0]
a = [13433L, 4747L, 17752L, 33060L, 31051L, 48809L, 29988L, 6421L, 20021L, 38888L, 24844L, 20706L, 11713L, 34938L, 12865L, 6085L, 37391L, 32840L, 31964L, 27194L, 8701L, 48142L, 27066L, 28626L, 37431L, 39142L, 46795L, 21771L, 44280L, 40628L, 35013L, 18583L, 5418L, 4347L, 43929L, 9934L, 46892L, 19868L]
b = [13711L, 7074L, 79833L, 42654L, 23241L, 41412L, 61795L, 6373L, 19304L, 1363L, 1682L, 66279L, 76134L, 60748L, 10355L, 63484L, 30491L, 34005L, 51393L, 38029L, 7241L, 4998L, 18562L, 16935L, 66677L, 51321L, 13771L, 49108L, 52166L, 8851L, 16900L, 31682L, 16684L, 12046L, 16764L, 64315L, 76742L, 14022L]
c = [832832835L, -924053193L, -307134635L, -527578092L, 998625960L, -715102211L, 3572182L, -963194083L, -475718185L, -361574731L, -678171563L, 107566155L, 608670527L, 254218946L, -81206308L, -284228457L, 373369420L, 659110852L, 165298084L, -389004184L, 893094421L, -868933443L, 44838205L, -98551062L, -59800920L, -575871298L, -748337118L, 696390966L, 427210246L, -266607884L, -555200820L, -594235119L, -233255094L, 229291711L, 711922719L, 14476464L, -783373820L, 892608580L]
d = []
#[NODE: 385]
for i in range(38L):
d(a[i] * data[i] * data[i] + b[i] * data[i] + c[i])
#[NODE: 452]
e = [973988289L, -867920193L, -132362266L, -172451190L, 1471255182L, -242282199L, 321870424L, -897049789L, -428663209L, -256350703L, -613466537L, 321254055L, 641759727L, 344601346L, -40281788L, -217030057L, 476060216L, 767746297L, 503093626L, -102198850L, 984358207L, -415480559L, 322813233L, 178032672L, 48876640L, -467362638L, -260077296L, 923436845L, 536082660L, -138702820L, -210365307L, -397666023L, -215329942L, 274852104L, 818217684L, 41479433L, -632022956L, 1204798830L]
p_s()
#[NODE: 594]
594
-1L
flag = sys(38L)
count(str2hex(flag))
虽然有反编译出来的结果有问题,但还是不错了的。
小结
使用基于图的表示法成功针对控制流平坦化进行了还原。虽然针对ollvm的解混淆已经有了,但是针对Python字节码的还没看到,所以也算是做出了自己的成果。













发表评论
您还未登录,请先登录。
登录