本篇翻译文章参加双倍稿费活动,活动链接请点此处
译者注
这是Aidan N. Gomez, Sicong Huang, Ivan Zhang, Bryan M. Li, Muhammad Osama, Łukasz Kaiser等人在ICLR 2018会议上的投稿,目前已经作为POSTER接收,主要介绍了利用GANs来破译移位密码(凯撒密码)和Vignere密码的技术,是目前比较少见的将GANs应用于离散型数据的例子。
本文主要是围绕着如何将GANs应用于离散型数据,前面部分涉及大量的GANs理论知识,翻译涉及到大量专业词汇,很多词汇目前都没有对应的中文翻译,考虑到文章的可读性和准确性,在一些词汇上直接使用英文。
摘要
这项工作详细地说明了“CipherGAN”——一个能够用于破译密码的框架。实验证明,CipherGAN能够高度准确地破译使用移位和Vigenere密码的语言数据,相比以前的方法,CipherGAN支持更多的词汇。在本文中,将介绍如何让CycleGAN与离散数据兼容,并以稳定的方式进行训练。最后,我们证明CipherGAN能够避免传统GANs应用于离散数据的误判问题。
1 、引言
早在古希腊人之前,人们就开始加密信息,同时,人们也沉迷于试图用暴力破解、频率分析、crib-dragging方法,甚至间谍活动等一系列方法来破译密码。在过去的一个世纪中,移位密码等简单密码的破译已经变得无关紧要,因为现代计算资源能够实现更安全的加密方案。由于密码破译需要攻击者对语言结构的深入理解,因此它仍然是一个有趣的问题。目前几乎所有的自动密码破译技术都必须依赖于“人”的存在,将自动化技术置于人类已有语言知识的基础上,以避免频率分析等简单算法所产生的错误。然而,在许多领域中,人工设计的特征常常被机器学习框架自动提取的特征所取代因此,要解决的问题如下:
神经网络是否可以在没有“人”参与的情况下自动地从文本中推导出隐藏的密码?
我们认为这种思考对于无监督翻译领域的影响将是深远的,从某种意义上说,每种语言都可以被看作是对另一种语言的加密。Copiale密码的破译便是将机器学习作为语言翻译来解码加密文本的一个很好的例子。在这种情况下,CycleGAN的架构是极具普适性的,在本文中我们证明了CipherGAN能够以极高的准确率破解密码,可以快速应用到由用户选择的加密算法生成的明文和密文组。
除了CipherGAN,我们还对以下技术进行研究:
- 我们从理论上描述和分析了阻碍GANs应用于离散数据的误判问题;
- 我们提出了一种通过在嵌入空间(embedding space)中进行计算以解决上述问题的方法,并展示了它实际中的工作。
1.1 移位密码和Vigenere密码
移位密码和Vigenere密码是众所周知的替代密码。人类使用替代密码的记录可以追溯到公元前58年,当时凯撒把一封信中的每个字母替换为字母后面三个字母。
如图1所示,“attackatdawn”可以被加密为“DWWDFNDWGDZQ”。这个消息可以快速被接收者解码,但对第三方来说则毫无意义。在此后的数百年中,这种移位密码保证了发送者和接收者的安全通信。第9世纪,polymath Al-Kindi引入了频率分析的概念。他通过分析个别字母的频率,使破译密码成为可能。例如,英文中最常出现的字母是’e’(12.7%),’t’(9.1%)和’a’(8.2%)。而’q’,’x’和’z’的频率都小于1%。此外,攻击者还可以关注重复的字母,例如’ss’,’ee’和’oo’是英语中最常见的。语言上的这种特征为攻击者提供了一种有效的破解方法。
但是多表代换密码,如Vigenere密码,能够避免通过n-gram频率分析来确定密码表的映射。这类加密算法进一步使用多个独立密钥的移位密码来对消息进行加密,使得其在长度上分别匹配明文。通过增加密钥长度大大增加了可能的组合数量,从而防止了基本的频率分析。19世纪,Charles Babbage发现可以通过计算密文中字母序列的重复和间隔确定密钥的长度。获得了密钥的长度,我们可以在对密码基数进行索引后应用频率分析。这种方法虽然可以破解Vigenere密码,但是不仅非常耗时,而且要求攻击者对语言本身具有的深入了解。
研究人员对自动化移位密码破解技术进行了大量的研究(Ramesh et al., 1993; Forsyth& Safavi-Naini, 1993; Hasinoff, 2003; Knight et al., 2006; Verma et al., 2007; Raju et al., 2010;Knight et al., 2011),其中很多都获得了非常好的成果。但这些都是人们从针对特定密码和词汇表通过人工算法实现的。针对多表代换密码的自动破解工作在小规模词汇表中也取得了类似的成功。但把以前的工作与我们进行比较是一件困难的事情,因为他们主要关注推断密钥、推断有限数量的密文(确定唯一性距离)、分析完成小部分密码映射所需的唯一性距离等方面。
相比以往的工作,我们具备了无约束密文语料库的优点。但是,我们自己规定了以下前提:我们的模型不具备任何关于词汇元素频率的先验知识和关于密钥的信息。因此,我们的工作必须克服的困难问题是我们的词汇表非常庞大,过去所有的工作只处理了大约26个字符的词汇表,而我们的模型囊括了超过200个不同词汇元素的词级密码。因此,与以前的工作相比,我们的方法最大的特点是“不干涉”(hands-off),可以很容易地应用于不同形式的密码、不同的基础数据以及无监督的文本对齐任务。
1.2 GANs & Wasserstein GANs
生成对抗网络(GANs)是Goodfellow等人提出的一类神经网络模型,用于在真实数据分布下优化似然度。GANs在一定程度上平衡了传统方法的过拟合和欠拟合问题。现有的研究表明GANs在图像生成领域具有强大的优势,但是在对于离散数据而言,GANs的支持不够完备。
Goodfellow等人在2014年提出的GAN判别器:
其中F是生成器网络,D是判别器网络。这里的损失(loss)容易受到“mode collapse”的影响,在这种情况下,将产生一个低多样性的生成分布。为了提高泛化能力,Wasserstein GAN(WGAN)使用了K-Lipschitz判别函数D : X → R和最小化地动距离(earth mover distance)。其中Lipschitz条件的实现依赖于修改判别器权重使其落入预定范围。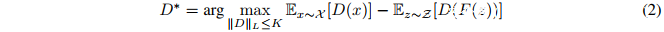
其中X^是对真实数据分布X和生成数据分布Xg = {F(z)|z ∼ Z}边界的采样。
1.3 CYCLEGAN
CycleGAN是一个用于无监督学习两个数据分布之间的映射的生成对抗网络。这三个论文中(Zhu等人,2017; Yi等人,2017年; Liu等人,2017)分享了我们下面描述的许多核心特征,为了简单起见,我们将CycleGAN作为我们工作的基础。它通过使用两个映射生成器和两个鉴别器来作用于分布X和Y。
CycleGAN优化了标准GAN损失函数LGAN:
同时也考虑了损失重建,Lcyc:
综合公式(4)、(5),利用超参数λ平衡损失函数:
这也就产生了进一步的训练目标:
CycleGAN利用Lcyc,保留了输入输出映射的重构来避免mode collapse。它在两个视觉上相似的不成对图像转换中展现出极好的结果。CipherGAN是这种无监督学习框架成功应用于离散数据(如语言)的第一个例子。
2 离散的GANs
目前,将GAN应用于离散数据生成仍然是一个值得关注的开放性研究问题。利用GAN训练离散数据生成器主要的困难在于在计算图(computation graph)中缺少通过离散节点的梯度。判别器可能会使用一个与重离散化(re-discretized)数据正确性无关的优化判别准则,生成离散输出的替代方法,比如在离散元素上生成分类分布(categorical distribution)的生成器,则容易产生误判问题。在我们关于离散元素的连续分布的例子中,生成的样本都位于k维单形(simplex)中,维数k等于分布中元素的个数。在这种情况下,来自真实数据中的样本总是位于 单形的顶点vi上,而任何次优的生成器将在单形的内部产生样本。在这个例子中,出现误判的判别器可以将评估样本是否在单形顶点上作为最优的鉴别准则,而这完全不受生成器新生成离散样本正确性的影响。
近年来,研究人员已经提出了许多用离散输出来训练生成器的方法:SeqGAN(Yu等人,2017)使用增强梯度估计来训练生成器;Boundary-seeking GANs(Hjelm等人,2017)和maximun-likelihood augmented GANs(Che等人,2017)提出了一种类似于REINFORCE(Williams,1992)估计的低偏差(bias)和方差的梯度近似。Gumbel-softmax GANs(Kusner&Hernandez’-Lobato,2016)将单形中的离散变量替换连续松散变量(continuous relaxation variable);WGANs(Arjovsky等人,2017)通过保证判别器对其输入变化率的约束来缓解误判问题。
我们的工作同时利用了Wasserstein GAN和Gumbel-softmax。我们在实现CycleGAN的过程中多次注意到该架构对初始化阶段敏感,需要多次重复尝试才能收敛到令人满意的映射(Bansal&Rathore,2017;Sari,2017)。将WGAN Jacobian范数正则化添加到判别器的损失函数之后,我们成功避免了这种的不稳定性。另外,我们发现如果把鉴别器放在嵌入空间(embedding space)中运行,而不是直接在生成器产生的softmax向量上运行,性能将有所提高。
我们的假设可以由下面的命题1来证明的,即由于在整个训练过程中进行了小噪声更新,所以嵌入向量(embedding vector)可以作为离散随机变量的continuous relaxation;命题1断言,如果用连续随机变量代替离散随机变量,判别器将不能任意逼近δ-函数分布。图2展示了一个简单的判别器,它将单一顶点标识为真实数据;很明显,缺乏正则化导致判别器坍塌到单形顶点,在每一处的梯度都接近零;而Wasserstein GANs利用Jacobian范数正则化产生的空间中覆盖了真实数据到生成数据低变化率(在单形的其余区域梯度仍然接近零);最后用连续样本来替换离散随机变量实现了更加平缓的过渡,提供了更强的梯度信号进行学习。
在1.3所述的循环损失(auxiliary cycle loss)是CycleGAN所特有的。这产生的额外影响是生成样本往往会远离鉴别器的最小值,以便更好地满足重建的映射。例如,判别器会偏好非双射的密码映射;在这种情况下,模型将会直接从循环损耗(cycle loss)中接收到一个强烈的信号,而不是来自判别器的最小值。由于WGAN的曲率正则化(见公式 3)从未在某个区域进行,这个区域的曲率就会趋近于零(如图2所示),而模型就会逆着从鉴别器接收到的梯度移动。
这里的“曲率”是指判别器输出相对于其输入的曲率,决定了生成器接收到的训练信号的强度。因此,低曲率意味着生成器很难获得用于提升的信息。这实现了在全局范围内获得强曲率的好处,而不是导致生成器样本和真实数据之间线性对立。Kodali等人提出将生成样本在各个方向正则化,这可能能够弥补我们面临的梯度消失问题;我们的实验证明,松弛的抽样技术是有效的。另外,Luc等人提出了一种类似于松弛抽样的方法,他们用真值(ground-truth)离散标注替代剩余的错误标注。
现在让我们来介绍命题1正式提出所需的定义:
下面的命题(在附录中证明)是该技术的理论基础:
3 、方法
3.1 CipherGAN
目前,将GANs应用于文本数据尚未产生真正令人信服的结果(Kawthekar等人)。先前使用GANs进行离散序列生成的尝试通常利用在token空间上输出概率分布的生成器(Gulrajani等,2017; Yu等,2017; Hjelm等,2017)。这导致判别器从数据分布中接收一系列离散的随机变量,并从生成器中接收一系列连续的随机变量;使得判别的任务变得微不足道,而且不会真正影响底层的数据分配。为了避免这种情况,我们通过允许生成器的输出分布来定义相应嵌入的凸组合(convex combination),使得判别器在嵌入空间中计算,由此产生了以下损失(loss):
我们在嵌入的WEmb和x中的one-hot向量之间以及由生成器F和G生成的embedding和softmax向量之间进行内积。前者相当于嵌入矢量表上的查找操作,而后者是词汇表中所有向量之间的凸组合。embedding WEmb在每个步骤被训练以使Lcyc最小化并使LGAN最大化,让嵌入易于被映射并容易区分。正如第2节所讨论的那样,上述损失函数的训练是不稳定的,每四个实验中就有三个未能产生正确的结果。这是CycleGAN在进行horse-zebra实验出现的一个问题,并且多次重现(Bansal&Rathore,2017;Sari,2017)。通过训练判别器损失、改进WGAN的Lipschitz条件,稳定性得到了显著提升,结果如下(DualGAN(Yi等,2017)通过修改权重来强制达到Lipschitz条件):
作为命题1的结论,对非平稳嵌入(non-stationary embeddings)进行训练的判别器将不能任意逼近δ-函数分布;这意味着对于X内的元素而言,存在某种“安全区”(safe-zones),在“安全区”内生成器可以有效“欺骗”判别器,防止发生误判。
在实验中,我们同时训练了嵌入向量作为模型的参数。嵌入向量的梯度更新在训练迭代之间引入噪声;我们观察到在初始训练步骤之后,嵌入向量倾向于保持在有界区域。我们发现,利用嵌入向量替换数据与执行命题1中描述的随机抽样具有相似的效果。
4 实验
4.1 数据
我们在实验中使用来自Brown English文本数据集的明文自然语言样本。我们生成2倍batch_size大小的明文样本,前半部分作为CycleGAN的X分布,后半部分通过选择的密码作为Y分布。
对于我们的自然语言明文数据,我们使用Brown English语料库,该语料库由57340个句子中的一百多万个词语组成。我们实验了词语级(word-level)“Brown-W”和字母级(character-level)“Brown-C”的词汇表。对于词语级的词汇表,我们通过选取频率最高的k个词语来控制表的大小,并引入了一个“Unknow”的记号来表示词汇表以外的词语。我们展示了使用word-level词汇表扩展到大型词汇表;而更现代的加密技术依赖于具有大量元素的S盒(substitution-boxes)。
4.2 训练
我们用Mao等人最初提出的平方差损失代替了对数似然损失。进行替换的原始动机是提高了训练的稳定性并避免了梯度消失问题。在这项工作中,我们发现了对训练稳定性的重要影响。
因此,我们总的损失函数是:
我们调整了生成器和判别器的卷积结构,用一维变量替换所有的二维卷积,并将生成器中的过滤器减少到1,进行逐点卷积。卷积神经网络最近被证明能够有效进行语言相关的工作,并且能够显著加速训练。生成器和判别器在嵌入空间中接收一系列向量;生成器在词汇表上形成softmax分布,而判别器输出一个标量。
在所有的实验中,我们都使用“1”作为循环损失的归一化系数。为了兼容WGAN,我们用batch归一化替换了layer归一化。我们训练使用Adam优化器 (Kingma & Ba, 2014) ,其中batch size为64,learning rate为2e-4,β1=0,β2=0.9。learning rate在2500步内以指数形式升至2e-4,之后保持不变。实验中使用了256维嵌入向量,并按照Gulrajani等人的建议,将WGAN Lipschitz调节参数设定为10。
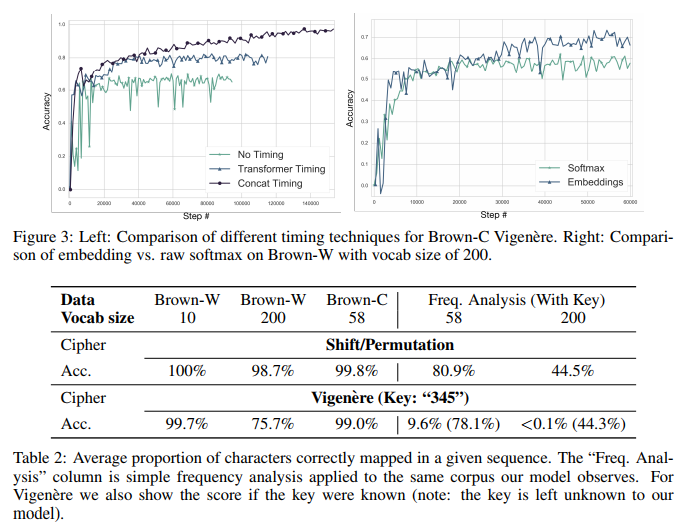
对于Vigenere密码,位置信息(positional information)决定了网络能否执行映射。我们尝试添加了Vaswani等人描述的timing signal。如图3所示,我们发现相对于没有明确的timing signal,性能有所提高(图3中的“Transformer Timing”);将学习位置嵌入矢量拼接到序列对应位置上能够进一步改善性能(图3中的“Concat Timing”),但这意味着该架构不能推广到比训练集更长的序列。对较长序列进行推广将是我们未来研究方向。
4.3 讨论
表2显示,CipherGAN在移位密码上具有接近完美的准确性,在3个词汇大小上都能快速解码。CipherGAN在Vigenere密码上也非常出色,在字母级取得了极好的结果,在词汇量为200的词语级上也取得了很好的结果。一个包含标点符号和特殊字符的字母级词汇表的大小为58,比以前要多一倍。与原始的CycleGAN相比,我们发现CipherGAN在训练中非常一致,并且对权值的随机初始化显然不敏感;我们把归因于Jacobian范数正则化项。
对于这两种密码,首先要确定的映射是那些最频繁出现的词汇,这表明程序确实在通过某种形式的频率分析来区分两个文本中的异常频率。另一个有趣的发现是程序犯的错误:程序经常会混淆标点符号,也许表明这些词汇元素的比较相似,导致在许多训练中观察到多次的混淆。
5 结论
CipherGAN显示了生成对抗网络应用于离散数据解决一些对细微差别极其敏感的困难任务。我们的工作有助于促进CycleGAN架构对于多类数据的无监督对齐任务的承诺。CipherGAN提出了一种训练中较为稳定的算法,改进了CycleGAN架构。实验证实,使用离散变量的continuous relaxation,不仅促进通过离散节点的梯度流动,而且防止经常出现到的误判问题。CipherGAN在结构上是非常通用的,可以直接应用于各种无监督的文本对齐。
参考文献
Martin Arjovsky, Soumith Chintala, and Leon Bottou. Wasserstein gan. ´ arXiv preprint arXiv:1701.07875, 2017.
Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E Hinton. Layer normalization. arXiv preprint arXiv:1607.06450, 2016.
Hardik Bansal and Archit Rathore. Understanding and implementing cyclegan in tensorflow. https://hardikbansal.github.io/CycleGANBlog/, 2017.
John M Carroll and Steve Martin. The automated cryptanalysis of substitution ciphers. Cryptologia, 10(4):193–209, 1986.
Tong Che, Yanran Li, Ruixiang Zhang, R Devon Hjelm, Wenjie Li, Yangqiu Song, and Yoshua Bengio. Maximum-likelihood augmented discrete generative adversarial networks. arXiv preprint arXiv:1702.07983, 2017.
William Fedus, Mihaela Rosca, Balaji Lakshminarayanan, Andrew M. Dai, Shakir Mohamed, and Ian Goodfellow. Many paths to equilibrium: Gans do not need to decrease a divergence at every step, 2017.
William S Forsyth and Reihaneh Safavi-Naini. Automated cryptanalysis of substitution ciphers. Cryptologia, 17(4):407–418, 1993.
W Nelson Francis and Henry Kucera. Brown corpus manual. Brown University, 2, 1979.
Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial nets. In Advances in neural information processing systems, pp. 2672–2680, 2014.
Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep Learning. MIT Press, 2016. http: //www.deeplearningbook.org.
Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, and Aaron Courville. Improved training of wasserstein gans. arXiv preprint arXiv:1704.00028, 2017.
Sam Hasinoff. Solving substitution ciphers. Department of Computer Science, University of Toronto, Tech. Rep, 2003.
R Devon Hjelm, Athul Paul Jacob, Tong Che, Kyunghyun Cho, and Yoshua Bengio. Boundaryseeking generative adversarial networks. arXiv preprint arXiv:1702.08431, 2017.
Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In International Conference on Machine Learning, pp. 448–456, 2015.
Eric Jang, Shixiang Gu, and Ben Poole. Categorical reparameterization with gumbel-softmax. arXiv preprint arXiv:1611.01144, 2016. 9
Nal Kalchbrenner, Lasse Espeholt, Karen Simonyan, Aaron van den Oord, Alex Graves, and Koray Kavukcuoglu. Neural machine translation in linear time. arXiv preprint arXiv:1610.10099, 2016.
Prasad Kawthekar, Raunaq Rewari, and Suvrat Bhooshan. Evaluating generative models for text generation.
Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. CoRR, abs/1412.6980, 2014. URL http://arxiv.org/abs/1412.6980.
Kevin Knight, Anish Nair, Nishit Rathod, and Kenji Yamada. Unsupervised analysis for decipherment problems. In Proceedings of the COLING/ACL on Main conference poster sessions, pp. 499–506. Association for Computational Linguistics, 2006.
Kevin Knight, Beata Megyesi, and Christiane Schaefer. The copiale cipher. In ´ Proceedings of the 4th Workshop on Building and Using Comparable Corpora: Comparable Corpora and the Web, pp. 2–9. Association for Computational Linguistics, 2011.
Naveen Kodali, Jacob Abernethy, James Hays, and Zsolt Kira. How to train your dragan. arXiv preprint arXiv:1705.07215, 2017.
Matt J Kusner and Jose Miguel Hern ´ andez-Lobato. Gans for sequences of discrete elements with ´ the gumbel-softmax distribution. arXiv preprint arXiv:1611.04051, 2016.
Ming-Yu Liu, Thomas Breuel, and Jan Kautz. Unsupervised image-to-image translation networks. arXiv preprint arXiv:1703.00848, 2017.
Pauline Luc, Camille Couprie, Soumith Chintala, and Jakob Verbeek. Semantic segmentation using adversarial networks. arXiv preprint arXiv:1611.08408, 2016.
Chris J Maddison, Andriy Mnih, and Yee Whye Teh. The concrete distribution: A continuous relaxation of discrete random variables. arXiv preprint arXiv:1611.00712, 2016.
Xudong Mao, Qing Li, Haoran Xie, Raymond YK Lau, Zhen Wang, and Stephen Paul Smolley. Least squares generative adversarial networks. arXiv preprint ArXiv:1611.04076, 2016.
SS Omran, AS Al-Khalid, and DM Al-Saady. A cryptanalytic attack on vigenere cipher using ` genetic algorithm. In Open Systems (ICOS), 2011 IEEE Conference on, pp. 59–64. IEEE, 2011.
Bhadri Msvs Raju et al. Decipherment of substitution cipher using enhanced probability distribution. International Journal of Computer Applications, 5(8):34–40, 2010.
RS Ramesh, G Athithan, and K Thiruvengadam. An automated approach to solve simple substitution ciphers. Cryptologia, 17(2):202–218, 1993.
Eyyb Sari. tensorflow-cyclegan. https://github.com/Eyyub/tensorflow-cyclegan, 2017.
Simon Singh. The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography. Anchor, 2000.
Ragheb Toemeh and Subbanagounder Arumugam. Applying genetic algorithms for searching keyspace of polyalphabetic substitution ciphers. International Arab Journal of Information Technology (IAJIT), 5(1), 2008.
Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Lukasz Kaiser, and Illia Polosukhin. Attention is all you need. arXiv preprint arXiv:1706.03762, 2017.
AK Verma, Mayank Dave, and RC Joshi. Genetic algorithm and tabu search attack on the monoalphabetic substitution cipher i adhoc networks. In Journal of Computer science. Citeseer, 2007.
Ronald J Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning, 8(3-4):229–256, 1992. 10 Zili Yi, Hao Zhang, Ping Tan Gong, et al. Dualgan: Unsupervised dual learning for image-to-image translation. arXiv preprint arXiv:1704.02510, 2017.
Lantao Yu, Weinan Zhang, Jun Wang, and Yong Yu. Seqgan: Sequence generative adversarial nets with policy gradient. In AAAI, pp. 2852–2858, 2017.
Xiang Zhang and Yann LeCun. Text understanding from scratch. arXiv preprint arXiv:1502.01710, 2015.
Jun-Yan Zhu, Taesung Park, Phillip Isola, and Alexei A Efros. Unpaired image-to-image translation using cycle-consistent adversarial networks. arXiv preprint arXiv:1703.10593, 2017.
附录
参见论文APPENDIX部分


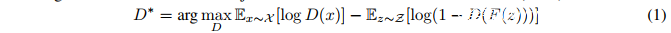
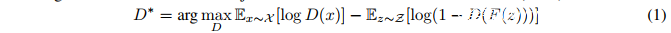
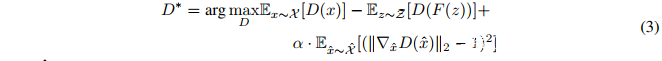
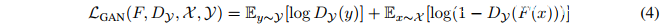
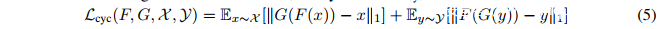
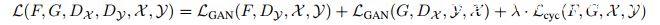
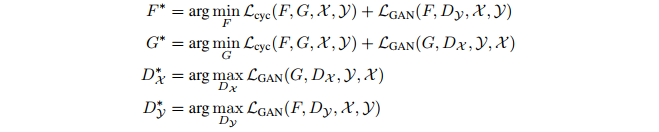



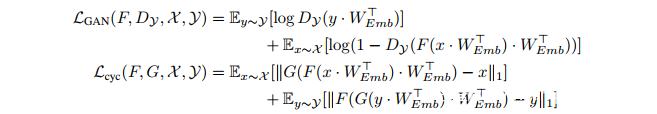
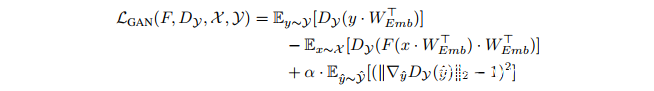
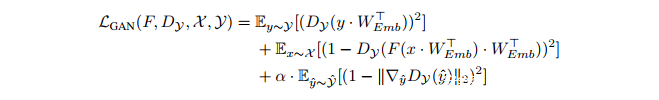
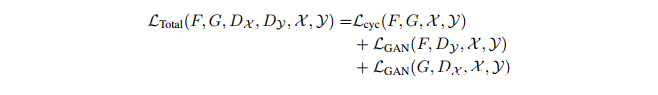






发表评论
您还未登录,请先登录。
登录