前言
前段时间研究了一下ECDSA签名的一些特性,发现确实有点意思,正好这个学期也开了密码学的课程,借着机会把ECC又研究了一番,今天就先初步探究一下利用Pohlig-Hellman算法来攻击椭圆曲线离散对数问题(ECDLP)。
ECDLP
概要
说实话,同样作为公钥密码学,相比较于RSA与DL,ECC确实是要难一些,不仅是解决问题的困难度上,学起来也是如此,从初学到深入你就越能体会到数学的奥妙
篇幅所限同时也是水平原因,相关的基础性知识这里就不涉及了,如果对于ECC并不了解的话建议看看这两篇文章ECC加密算法入门介绍,ECC椭圆曲线详解
我们知道ECC相比于其他的公钥算法而言具有更高的单位比特强度,同时运算速度也更快,这意味着可以用更短的密钥以及更高的性能来完成需求,在很多领域也已经派上了用场,近年来大热的区块链也有很多地方采用了它作为签名算法,所以说研究研究还是挺有必要的
什么是椭圆曲线离散对数问题
我们不妨先来看看什么是离散对数问题
对于整数域来说,其实就是对于给定的式子
y = g^x mod p
当仅知道g,p与y时我们是很难求得x的值的
而在椭圆曲线上,就是对于一个给定的椭圆曲线E,当我们设定了一个阶为n的基点G后,在[0,n-1]上选取一整数k,由式子Gk = Q,当我们仅知道G与Q时,想反推得到k是困难的,这就是椭圆曲线上的离散对数问题
不过有意思的是其实ECDLP的困难目前还没有得到数学上的证明,因此事实上它目前还只是一个假设
当然了,离散对数问题是难解但也并非是无解,如果你尝试直接爆破的话那么复杂度当然就直接视为n了,但是在某些情况下也有一些方法可以帮助我们降低解决问题的复杂度,特别是当算法取了一些不安全的特殊值时,比如一些不安全的p以及不安全的椭圆曲线,这些都会成为我们攻破密钥系统的利刃,而一个相对安全的密钥系统就要努力避开生成对应的参数
Pohlig-Hellman攻击方法
其实对ECDLP的攻击手法还是比较多的,近年来研究也还在不断进行,新的攻击方法也在不断提出,更多的方案可以参见此博文,传送门,目前来讲最有效的方法应该还是将Pohlig-Hellman 算法和 Pollard’s rho 算法结合,这样所需的时间复杂度大概为O(p1^(1/2)),其中p1是阶数n的最大素因子,相应的为了对抗这类攻击就要求生成参数时得到的n含有较大的素因子,或者n自身就是一个大素数就更好了,至于其他的攻击手法则大多是在曲线参数取值特殊的情况下可以极大缩小复杂度的方法,比如对超椭圆曲线有效的MOV方法,所以要生成一个安全的椭圆曲线就必须绕过这一系列的特殊情况
接下来我们看看Pohlig-Hellman,如它的名字所示,该算法由Pohlig和Hellman发明,这是一种为解决离散对数问题而提出的攻击方法,早在1978年就被提出,比椭圆曲线的提出时间还早,它的主要思想是对阶数进行分解,比如整数域中y = g ^ x mod p里的x以及椭圆曲线 离散对数问题中Gk = Q 的G的阶n,这样就把对应的离散对数问题转移到了每个因子条件下对应的离散对数,这样就可以利用中国剩余定理进行求解,下面我们就研究一下椭圆曲线下的Pohlig-Hellman算法
首先我们不妨假设需要求解的式子为
Q = l * P
其中P为我们选取的一个基点,l就是我们选定的随机数,相当于要求解的私钥
首先求得P的阶n,也就是可使得n*P不存在的最小正整数
然后我们将n进行分解,我们设
n = p1^e1 * p2^e2 ……pr^er
然后我们将这些因子拿出来,对于i属于[1,r],计算
li = l mod pi^ei
于是我们便得到了下面的这一系列等式
l ≡ (l1 mod p1^e1)
l ≡ (l2 mod p2^e2)
……
l ≡ (lr mod pr^er)
看上去是不是有点眼熟,如果得到了这些li的值我们就能使用中国剩余定理进行求解得到l了,现在的问题就是求解这些li
首先我们将li设为成pi表示的多项式,如下
接下来我们的任务就是求解这些z,注意这里的z应该是属于[0,pi-1]
下面就很有意思了,为了计算zi,我们分别取P0和Q0,并取值
这样我们就有了pi*P0 = nP,接下来我们可以得到Q0的表达式
其实就是在我们原表达式的两边乘上了n/pi
这样的话我们再转回li,先求解z0
这时我们便将在P域上的离散对数分解到了P0域上,因为P0的阶是n/pi,已经较原本的阶n运算的复杂度小了很多,当然,除非n本身就是个大素数
在这里我们可以求得z0,然后我们再代回原式
此时就可以求解z1,然后依次将zi全部算出来,这样我们就得到了l1,然后便可以代入前面的等式,将li都求出后即可利用中国剩余定理求出l
说实话确实有点绕,我也是懵逼了一半天,同时要注意这里的运算都是基于椭圆曲线的,虽然道理是相通的但是在具体的运算里还是完全不同,在理解的时候还是需要注意,不过确实我也水平有限,写的可能不是太清楚
一道题目
这是picoCTF 2017的一道crypto题目,恰好考点就是这个Pohlig-Hellman,所以也拿出来讲两句,内容与write up链接可见此,传送门
主要是这道题目确实让我体会到了sagemath工具的强大,什么都帮你内置好了,你就直接用就行了
开始时先让我们算b,这很简单,就不多说了,得到需要的参数后我们有了如下的椭圆曲线
M = 93556643250795678718734474880013829509320385402690660619699653921022012489089
A = 66001598144012865876674115570268990806314506711104521036747533612798434904785
B = 25255205054024371783896605039267101837972419055969636393425590261926131199030
P = (56027910981442853390816693056740903416379421186644480759538594137486160388926, 65533262933617146434438829354623658858649726233622196512439589744498050226926)
Q = (61124499720410964164289905006830679547191538609778446060514645905829507254103, 2595146854028317060979753545310334521407008629091560515441729386088057610440)
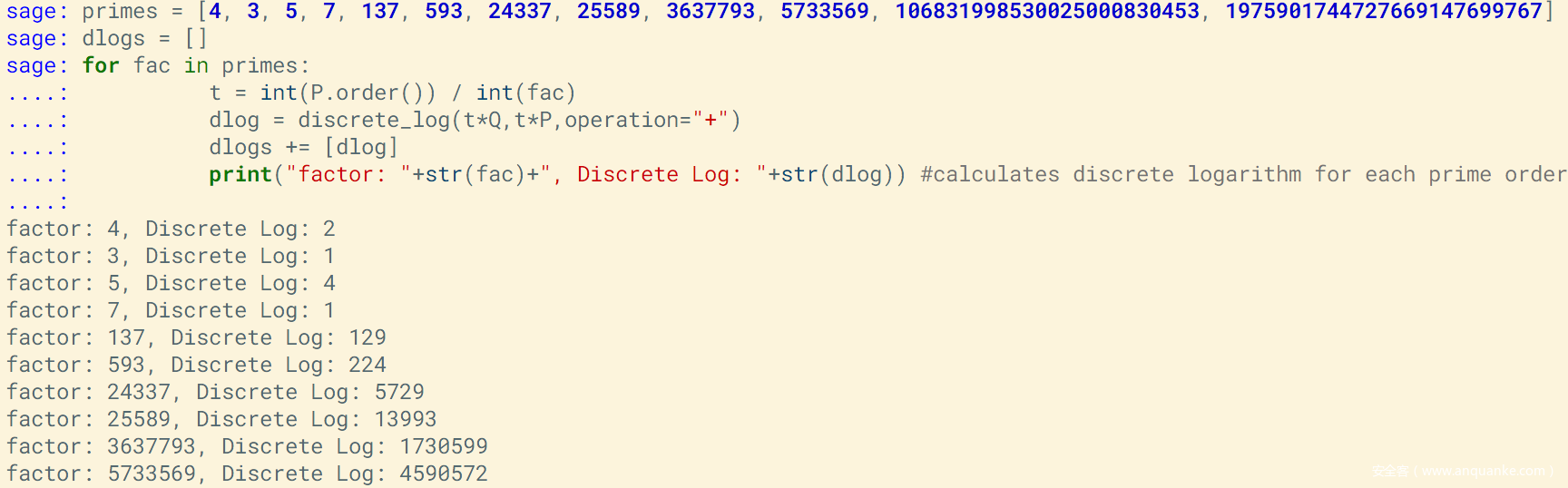
按照我们前面所讲的,首先求得P的阶,然后将其分解,这点sage都可以直接帮我们完成
然后任务其实就是求分解后对应的阶下也就是P0对应的li了,这个我们也可以用sage里的discrete_log函数来直接完成,真的是好用到不行
可以看到有两个阶的li没有算出来,不过这并不影响我们得到结果,得到了这些以后我们就可以利用中国剩余定理来求解了,而这也可以直接在sage里使用crt函数来调用,可以说是非常舒服了
原理没弄懂也没关系,会灵活运用工具照样也能玩得溜啊
写在最后
对于ECDLP的攻击方式还是有很多的,我目前也只是处于初学阶段,文章里可能有很多地方没写到位或者错误,希望大佬们多多指教
参考
http://wstein.org/edu/2010/414/projects/novotney.pdf
https://koclab.cs.ucsb.edu/teaching/ecc/project/2015Projects/Sommerseth+Hoeiland.pdf


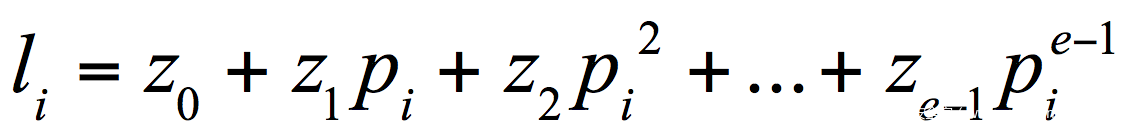
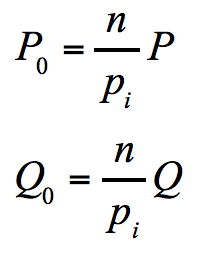
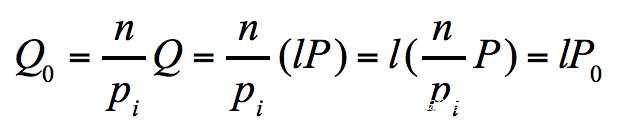
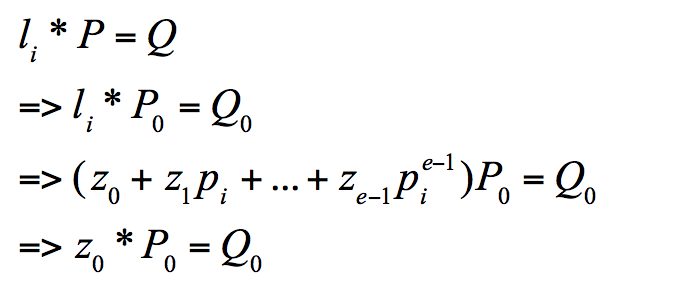
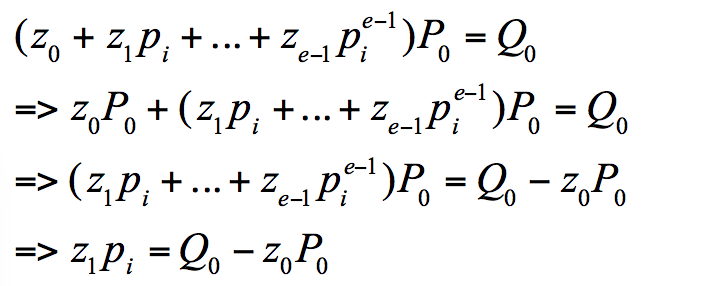









发表评论
您还未登录,请先登录。
登录