最近比赛繁多,抽时间看了一下EdDSA签名的有关内容,正好碰到一道题目涉及了对其的故障攻击,确实非常有意思,就在这里记录一下
EdDSA签名
EdDSA也是基于ECC的签名算法,平常我们见的比较多的应该是ECDSA签名,比如比特币使用的基于曲线secp256k1的ECDSA签名,以及基于NIST选择的几条曲线的签名等等
不过NIST P-256曲线,也就是secp256r1,因为默认使用的Dual_EC_DRBG随机数生成器一直被怀疑存在NSA隐藏的后门,到了13年斯诺登的曝光更是将这件事推上了风口浪尖,所以大家也就失去了对这一算法的信任,所以当年比特币选择了比较小众的secp256k1曲线还是有自己的考量
另外,我想熟悉ECDSA签名的朋友应该也都知道ECDSA签名算法的安全性是比较依赖于安全的随机数生成算法的,如果随机数算法存在问题,使用了相同的k进行签名,那么攻击者是可以根据签名信息恢复私钥的,历史上也出过几次这样的事故,比如10年索尼的PS3私钥遭破解以及12年受java某随机数生成库的影响造成的比特币被盗事件,关于这部分内容我也写过相关的分析,可以参见利用随机数冲突的ECDSA签名恢复以太坊私钥,所以说ECDSA签名在设计上还是存在一些问题的, 这也激励了新的EdDSA算法的出现
EdDSA签名算法由Schnorr签名发展变化而来,可以在RFC8032中看到它的定义实现,由曲线和参数的选择不同又可以划分为Ed25519和Ed448算法,顾命思义,它们两分别是基于curve25519和curve448曲线,一般用的比较多的是Ed25519算法,相比Ed448而言运算速度要更快,秘钥与签名空间也较小,二者的使用场景还是有点区别,下面我们主要讲的也是Ed25519
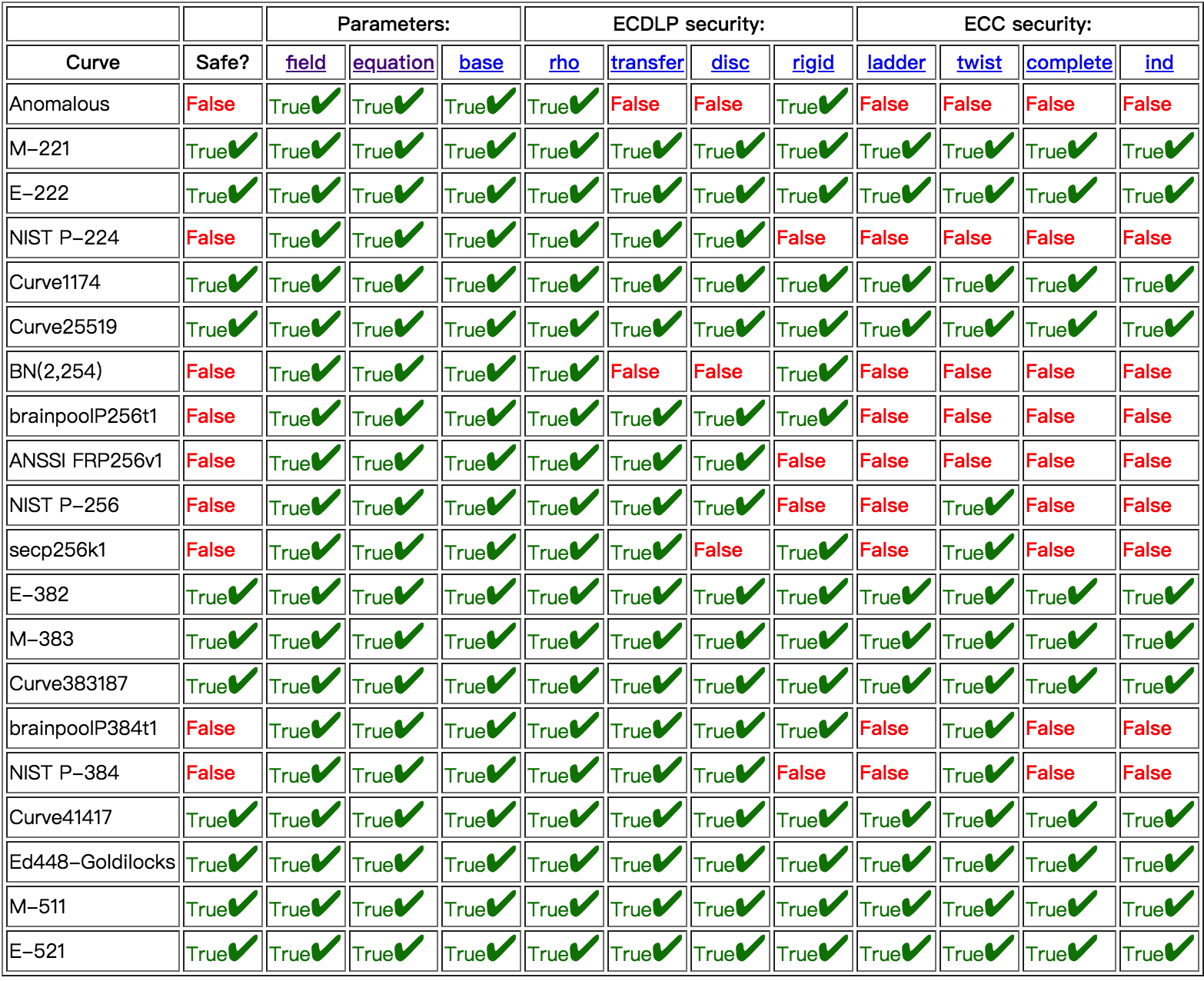
Ed25519所使用的曲线由curve25519变换而来,curve25519是蒙哥马利曲线,经过变换得到Ed25519使用的扭爱德华曲线edwards25519,curve25519曲线的安全性是非常高的,可以在safecurves查看各椭圆曲线的安全指标,curve25519是其中为数不多所有指标都达标的曲线,curve25519常用于密钥交换的DH算法
而且EdDSA的运算速度也比ECDSA算法要快很多,优势可以说是非常明显的,门罗币和zcash等加密货币已经将算法切换到了EdDSA了,目前其也被确认为下一代椭圆曲线算法
Ed25518所取的有限域P跟curve25519相同,都是2^255-19,这也是这一曲线的名字由来,还有很多其他参数如公私钥的长度,选取的基点B等,在不同情况下也有不同的选择,Ed25519中也可做进一步的划分,只要满足rfc文档的定义即可,更多参数的定义可以参考rfc7748
下面我们来看看Ed25519的具体签名过程,相比ECDSA确实有很大区别
Ed25519的私钥k长度为b bit,一般是256,其使用的hash算法H的输出长度为2b bit,一般选择的是SHA512,对应b等于256
首先,对私钥k进行hash,得到
使用hash的结果我们可以计算得到参数a
这样我们就可以得到私钥k对应的公钥A,A=aB,B为选取的基点,下面我们准备对消息M进行签名,过程如下,其中l为基点B的阶
这样就得到了消息M的签名(R,S),签名的验证则需满足下面的等式
观察整个签名过程,我们不难发现,一个私钥k,当对同一个消息M进行签名时R与S都是固定的,所以说EdDSA是一种确定性的签名算法,不像ECDSA那样每次签名都根据选取的随机送的变化而不同,所以EdDSA的安全性也就不再依赖于随机数生成器
Ed25519的实现程序可以参考这里,Ed25519 software,用python实现的,还是挺有意思
fault attack
下面我们简单介绍一下fault attack也就是故障攻击,更确切地说我们也可以叫它差分错误分析(Differential fault analysis),算是侧信道攻击的一种,主要针对包含处理器的智能卡,手法是通过物理方法,如电磁辐射,激光等干扰密码芯片的正常工作,迫使其执行某些错误的操作,依据错误的信息能够有效推算出密码系统的密钥信息
其实故障攻击的出现也是一场意外,科学家在研究时发现一块芯片的敏感区域在遭受放射性的照射后出现了比特位翻转的现象,从而引发了故障,但是通过分析这些信息却给我们打开了新世界的大门
引发故障的手法有很多种,比较简单的像是改变电压与温度,修改时钟频率,高级点的像是电磁辐射,激光照射等,还有一些对应的防御手段及应对的算法,这里就不展开了,有兴趣的可以看看这篇论文,A SURVEY ON FAULT ATTACKS
相对而言比较出名的应该是针对RSA签名的故障攻击,为提高RSA处理数据的速度,Quisquater等人利用中国剩余定理改进了RSA算法的运算速度,即CRT-RSA算法,不过这也为故障攻击的分析提供了绝佳的入口,感兴趣的可以看看这篇文章,RSA 签名故障分析
另外,DES和AES也早已有对应的攻击方式被提出,对于ECC的故障攻击也已经有了很多的研究,fault attack的威胁还是非常大的,而且攻击的方式其实也是非常巧妙
因为ECC算法对应的密钥空间较小,加之新的EdDSA的运算速度也比较快,所以在智能卡领域ECC也已经有了很多的应用,对应的故障攻击的威胁也就需要得到重视
下面我们就来看看针对Ed25519的故障攻击
fault attack on EdDSA
这部分内容主要是基于Kudelski的这篇研究,HOW TO DEFEAT ED25519 AND EDDSA USING FAULTS
前面我们也提到了EdDSA签名的特点是对于同一消息M,不论你对它签名多少次,得到的签名结果都是相同的,那么我们的fault attack也正是针对这一特性
在上面的前面过程中,假设我们针对第四步的hash过程进行攻击,这样就得到了一个错误的h值,即h’,由它计算得到的就是错误的签名值S’,那么根据关系我们就可以得到
要求出a,在上式中只有h’是未知的,那么我们如何知道h’的值呢,其实很简单,也就是爆破,关键在于我们要想办法在攻击时让hash计算得到的结果中某一位进行翻转,具体哪一位是未知的,翻转的结果也是未知的,所以我们就进行逐字节的爆破,在这里假设使用的算法中得到的h是32字节的,那么爆破过程可以用下面的伪代码表示,这也是借用了Kudelski的图
过程还是很好理解的,那么成功得到h’的值以后我们就可以计算得到a了,然而这时候你再看就会发现貌似知道了a也跟私钥没啥联系啊,进行签名的第一步我们得知道私钥的hash的后b位才能跟我们想签署的消息M生成新的h
其实这里利用的就是EdDSA签名的特点,也是这个故障攻击最巧妙的地方,我们不妨随机选择一个r值,不用管签名第一步计算的h,然后使用这个r完成下面的签名过程,得到了签名(R,S),然后进行签名校验
仔细查看整个推导过程,我们不难发现哪怕我们选择的r只是个随机值,但是签名的验证仍然是可以通过的,也就是说只要知道了a的值我们就可以进行签名的伪造了,并不需要知道原本的私钥,其实这里a已经可以看作是私钥了
可以看到对EdDSA进行故障攻击的过程是非常有趣的,以前提出的很多针对ECDSA的故障攻击多是针对运算过程中的基点进行攻击,比如让它的坐标发生改变,这样对应的基点的阶也将发生改变,很可能从一个大素数变成了一个大合数,而椭圆曲线的安全性要求基点的阶是素数,所以攻击后算法所使用的椭圆曲线其实以及不再安全了,很可能遭受算法如Pohlig-Hellman的攻击,这个我之前也写过相关的介绍,简析ECC攻击方法之Pohlig-Hellman
最近Kudelski自己举办了一场crypto的ctf,其中就有一道题目是关于Ed25519的fault attack,下面我们就一起来看看
fault attack challenge
比赛详情在这里,https://github.com/kudelskisecurity/cryptochallenge18
涉及的题目是challenge1,题目给了四个api,如下
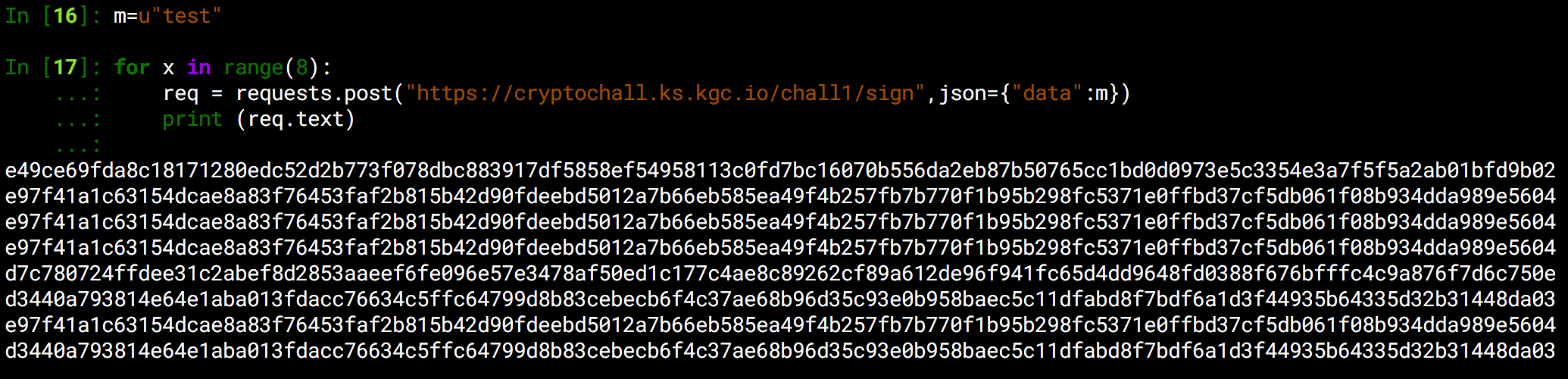
sign将返回我们发送的data的签名,我们来看看签名的情况
很有意思,签名的值在变化,其中穿插着一些错误的签名,重复出现的应该就是正确的签名了,不过观察那些错误的签名我们发现它们跟正确签名的R与S都不同,如果按照我们前面介绍的故障攻击的结果,那么应该是R相同而S不同,那么显然这里跟前面是不一样的,此处使用的fault attack是签名过程中第一步的hash值h进行了攻击,这样后面得到的R与S都是错误的,其实这样反而更简单了
回顾前面a的计算,当时我们未知的数是h’,但是在这里h’我们是可以直接通过错误的签名中的R’计算出来,所以说直接是已知的,那么我们就可以直接计算得到a了
查看一下我们需要签名的消息
完整的脚本可以参考Ledger-Donjon团队的脚本,以及他们的write up,其中的公钥可以通过计算得到的a跟基点B计算得到
写在最后
这次的研究让我又学到了不少新的东西,深切体会到了知识面的重要性,以前对于EdDSA都没什么了解,不过目前的趋势已经是在转向确定性签名机制了,EdDSA作为其中的代表自然是非常重要的,毕竟它的安全性和速度有目共睹
文章参考了很多的资料,就不一一列举了,重要的资料我都在文中添加了链接,同时水平有限,可能有些地方没写好甚至是出现错误,还希望师傅们多多指教


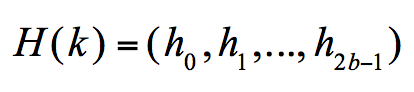
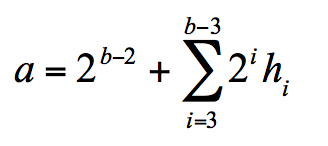
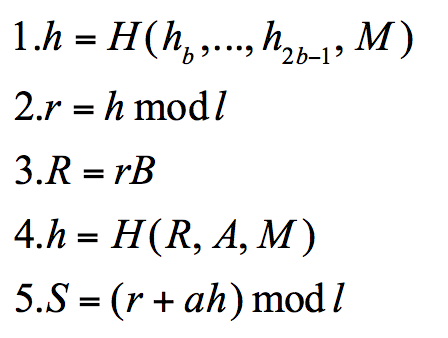
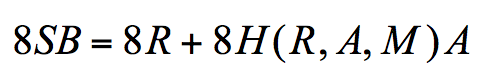
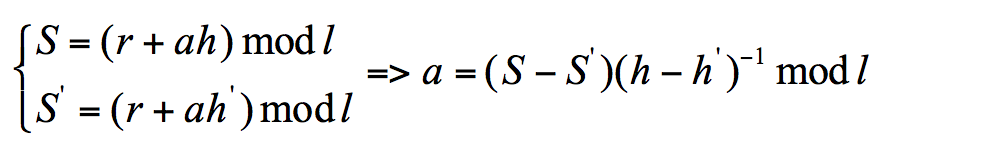

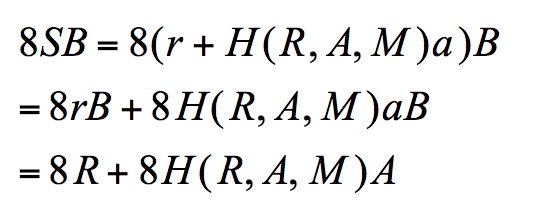









发表评论
您还未登录,请先登录。
登录