前言
隐写术本来被用于隐藏机密信息,但自从恐怖分子利用隐写术向数字图像中嵌入秘密指令发动美国双子塔的袭击(即著名的“9.11”事件)后,人们意识到了检测并分析隐写信息的重要性,目前隐写分析还处于检测载体中是否隐藏有机密信息的阶段。本文分析目前研究情况后,提出了一个隐写分析的卷积神经网络模型,它具有良好的隐写分析性能。
隐写术
图像隐写术是一门通过修改图像像素或频率系数在图像中隐藏秘密消息的技术和科学。隐写术最重要的要求是不可检测性,这就要求隐写方法将消息嵌入到数字载体时,生成的对象在视觉和统计上类似于原始载体。
隐写算法的一个重大分支是空间域隐写算法。在空间域方面,隐写算法的特点是直接改变图像的某些人眼难以察觉的像素点。典型的是最低有效位(LSB)替换,它将消息嵌入图像像素的最低有效位,但极易被检测。LSB替换可以被看作是非自适应隐写算法,这意味着数据隐藏后的修改像素将随机分布在整个图像上。然而,根据已有知识可知,位于纹理区域中的像素具有比平滑区域中的像素更好的隐藏属性,这一事实已被用于目前流行的自适应隐写算法中。
自适应隐写算法
自适应隐写算法自动识别图像内容的纹理区域隐藏秘密信息。例如边缘自适应隐写术(EA)根据两个相邻像素之间的差异将秘密消息嵌入边缘区域。目前流行的自适应隐写算法有HUGO、HILL、MiPOD、S-UNIWARD和等。它们在最小化失真函数的框架下进行了设计,即首先为载体图像中的每个像素分配嵌入成本,再根据嵌入成本定义失真函数,最后通过某些编码技术使失真函数最小化来获得生成的载密图像。实践证明,隐写算法的安全性越来越强,对它们的检测难度越来越高。
隐写分析
传统隐写分析算法主要基于手工提取的特征,常用的特征提取方式有小波直方图特征、马尔可夫特征、离散余弦变换系数的共生矩阵特征等。空域富模型(SRM)凭借其优越的特征提取方式被公认为传统隐写分析领域最成功的空域隐写检测算法。该模型主要针对相邻像素相关性设计,通过78个滤波器获取相邻像素残差,在此基础上产生高维特征向量。该模型能够检测三个空域算法,分别是,基于内容自适应隐藏的HUGO算法,基于边缘自适应的EA算法,和基于最优三元编码的±1调整类算法。SRM的详细内容如下。
SRM
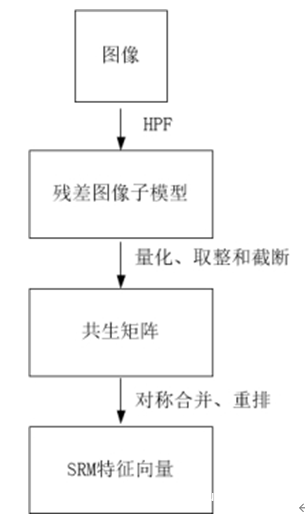
上图是SRM隐写分析特征的提取方法。首先通过高通滤波器获取残差图像子模型,再通过量化、取整和截断提取每一幅残差图像子模型的四阶共生矩阵,最后将这些共生矩阵的元素重新排列构成隐写分析特征。
SRM设计了丰富多样的空域高通滤波器,并使用这些滤波器对图像进行滤波,结果得到丰富多样的残差图像子模型,这些残差图像子模型可看做是高通滤波后的图像,主要包含了图像的高频成分。SRM使用丰富多样的残差图像子模型主要有两个原因,第一个是残差在很大程度上抑制了图像内容,减小了动态变化的范围,使得统计特性更加紧凑和健壮。第二个是对图像的某个像素的隐写嵌入改动可能会导致某些残差图像相应位置的相邻像素相关性发生变化,但未必能导致另一些残差图像的相应位置的相邻像素相关性发生变化,单独使用某一幅残差图像不能全面地反映所有可能的隐写嵌入改动引起的图像相邻像素相关性变化。
因此,SRM设计的丰富残差图像子模型能更全面地感知隐写引起的图像相邻像素相关性的变化。SRM的残差图像子模型公式如下:
残差主要包括一阶、二阶、三阶、SQUARE、EDGE3x3与EDGE5x5六类残差。如下为经典的残差和高通滤波器。水平、垂直、对角线、反对角线方向的残差表示为Rh,Rv,Rd,Rm。
线性残差
对于线性残差而言,上图已给出一阶、二阶、三阶线性残差的计算方式,以此类推,不难发现,SQUARE、EDGE3x3与EDGE5x5线性残差只是在计算中使用了更多方向的邻域像素。SQUARE、EDGE3x3与EDGE5x5高通滤波器如上图。在实践中,线性残差的计算方法通过分配率运算可转换为图像和高通滤波器的卷积运算,如下:
i,j表示待求取残差的像素位置,r、c表示运算的像素点位置。
隐写分析模型
近几年,随着GPU(Graphics Processing Unit)并行计算方式和深度学习的发展,可以模拟手工提取特征的方法从数据本身学习隐写信息。
本文利用了深度学习的技术模拟了SRM中线性残差的手工提取方法进行隐写信息的检测与分析。
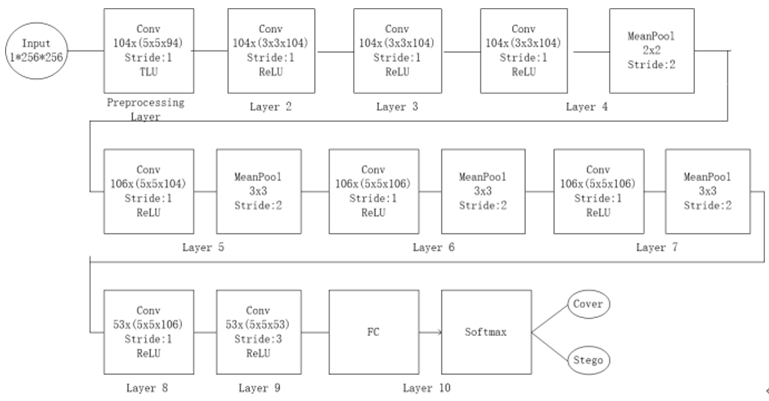
设计的基本网络模型结构如下。
模型接收大小256×256的图像,输出两类标签。CNN由许多层组成,其中包括一个图像预处理层、八个卷积层用于特征提取,一个全连接层用于结果分类。
隐写分析模型重点部分
在图像预处理层中,本人模拟了SRM中线性残差的手工提取方法。具体来说就是设计了一个通道数为30、大小为5×5的矩阵作为卷积核,使用SRM中收集的30个HPFs初始化此卷积核,然后将此卷积核与原图像做卷积运算,即得到线性残差信息,它包含了丰富的隐写信息。
本人选取的30个高通滤波器为:
[[[[ 0. 0. 0. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. -1. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 1. 0.]
[ 0. 0. -1. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. -1. 1. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. -1. 0. 0.]
[ 0. 0. 0. 1. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. -1. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. -1. 0. 0.]
[ 0. 1. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 1. -1. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0.]
[ 0. 0. -1. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. -2. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 1. 0.]
[ 0. 0. -2. 0. 0.]
[ 0. 1. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 1. -2. 1. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0.]
[ 0. 0. -2. 0. 0.]
[ 0. 0. 0. 1. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. -1. 0. 0.]
[ 0. 0. 3. 0. 0.]
[ 0. 0. -3. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[0. 0. 0. 3. 0.]
[0. 0. -3. 0. 0.]
[0. 1. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 1. -3. 3. 0.]
[0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0.]
[0. 0. -3. 0. 0.]
[0. 0. 0. 3. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. -3. 0. 0.]
[0. 0. 3. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0.]
[0. 0. -3. 0. 0.]
[0. 3. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 3. -3. 1. 0.]
[0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[0. 3. 0. 0. 0.]
[0. 0. -3. 0. 0.]
[0. 0. 0. 1. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[0. -1. 2. -1. 0.]
[0. 2. -4. 2. 0.]
[0. -1. 2. -1. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[0. -1. 2. -1. 0.]
[0. 2. -4. 2. 0.]
[0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[0. 0. 2. -1. 0.]
[0. 0. -4. 2. 0.]
[0. 0. 2. -1. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 2. -4. 2. 0.]
[0. -1. 2. -1. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. -1. 2. 0. 0.]
[ 0. 2. -4. 0. 0.]
[ 0. -1. 2. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ -1. 2. -2. 2. -1.]
[ 2. -6. 8. -6. 2.]
[ -2. 8. -12. 8. -2.]
[ 2. -6. 8. -6. 2.]
[ -1. 2. -2. 2. -1.]]]
[[[ -1. 2. -2. 2. -1.]
[ 2. -6. 8. -6. 2.]
[ -2. 8. -12. 8. -2.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
[[[ 0. 0. -2. 2. -1.]
[ 0. 0. 8. -6. 2.]
[ 0. 0. -12. 8. -2.]
[ 0. 0. 8. -6. 2.]
[ 0. 0. -2. 2. -1.]]]
[[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ -2. 8. -12. 8. -2.]
[ 2. -6. 8. -6. 2.]
[ -1. 2. -2. 2. -1.]]]
[[[ -1. 2. -2. 0. 0.]
[ 2. -6. 8. 0. 0.]
[ -2. 8. -12. 0. 0.]
[ 2. -6. 8. 0. 0.]
[ -1. 2. -2. 0. 0.]]]]将它们先存储到数组SRM_Kernels中,在定义变量卷积核W_SRM时,使用数组SRM_Kernels初始化变量,如下:
W_SRM = tf.get_variable('W', initializer=SRM_Kernels, dtype=tf.float32, regularizer=None)
隐写分析模型性能测试
本文应用了两个著名的内容自适应隐写算法来评估隐写分析模型的性能,即WOW、S-UNIWARD,使用拥有10000张图片的图像集BOSSBase 1.01,将其图像缩放为256×256后做隐写操作。随后即有10000对原图、隐写图,选择8000对做训练,剩余的各1000对做验证和测试。
结果如下表,数据表示隐写分析的准确率。
上图中,SRM+EC代表传统的手工提取特征的隐写分析模型,看结果可知,本文的模型对两种隐写算法的检测准确率都很高,超过了传统的隐写分析模型,具备良好的效果
基于线性及非线性残差特征学习
在模拟线性残差进行隐写特征的学习时,可发现一个线性残差特征仅仅表现极少的目标位置邻域像素的相关性变化,提取出的特征信息有限,而非线性残差特征能有效地弥补这个缺陷。因此,本文模拟线性及非线性残差进行隐写特征的学习,提出了新的卷积神经网络隐写分析模型,它具有更佳的隐写分析性能。
空域隐写分析新阶段发展历程
传统隐写分析算法基于手工特征的提取,典型代表是空域富模型SRM。在其后相当长一段时间内,学者们提出了一系列改进的隐写分析算法,但仍然沿用SRM相邻像素相关性的核心思想和特征的获取方式,因此没有产生意义重大的隐写分析成果。如今,SRM通过不断改进的高通滤波器已能从数据中提取三万多维特征,然而这些高通滤波器的设计大多基于经验,缺乏严谨的论证和分析。有学者认为从数据本身学习特征会更有效,随后越来越多的学者支持并尝试实现这一理念,在GPU和深度学习的支持下,隐写分析进入了新阶段。
2014年,Tan和Li提出了第一个应用深度学习技术的隐写分析模型,它使用基于自编码器的卷积神经网络(CNN)进行无监督学习。随后,学者们使用高通滤波器(HPF)对图像进行预处理,从而提高嵌入过程引入的隐写噪声的影响,并进行监督学习。2015年,Qian等人提出了第一个采用监督学习方法的卷积神经网络模型。Xu等人提出了一个类似于Qian的CNN模型,不同的是,他们使用了一个绝对值层(ABS)和1×1的卷积核来加强统计建模。2017年,Xu等人在ResNet的启发下,提出了一个新的CNN模型,它由20个卷积层组成。Ye等人提出了一个由8个卷积层组成的空域CNN模型,它在预处理层添加了截断线性单元(TLU)激活函数和一组滤波器,这组滤波器基于SRM,被用于初始化预处理层的卷积核,以获得线性残差特征图。2017年主要的趋势是应用ResNet等优化了卷积神经网络架构,同时模拟了SRM的特征提取方式,显著提高了隐写分析的检测效果。2018年,Yedroudj等人提出了一个由5个卷积层组成的空域CNN模型,该模型使用了基于SRM特征提取方式的高通滤波器作为预处理层的卷积核,并且在每一个卷积层中都加入了BN。Zhang等人提出了新的CNN模型,它使用深度可分离卷积网络获得特征图通道和空间的相关性,加入spatial pyramid pooling(SPP)处理不同大小的图像,提高了特征表达的能力。
在空域中,模拟传统SRM的手工提取线性残差特征的方法,学者们提出的隐写分析模型使用深度学习技术从载密图像中学习了更丰富的隐写噪声,取得了优于SRM的准确率。
现有的空域隐写分析CNN模型都基于线性残差特征进行隐写分析,这些线性残差特征线性地组合了多滤波器操作的残差信息。而SRM研究表明,对多滤波器操作的残差信息进行非线性组合同样能有效地抑制图像内容的干扰,放大隐写痕迹。
SRM的非线性残差
上一篇文章已经描述了SRM中线性残差的详细计算方法。对于非线性残差而言,如下图所示,它可通过求取两个或者更多同类线性滤波残差的最大值或最小值得到。其中,Rij表示某一像素坐标为(i,j)的残差信息,水平、垂直、对角线、反对角线方向的残差表示为Rh,Rv,Rd,Rm。
以一阶残差为例,要获得一阶非线性残差,首先通过计算获得所有一阶线性残差,再统计其最大最小值即求得两个一阶非线性残差。下图是一阶线性残差原型,yij即待求取残差位置的像素值,yi,j+1即待求取残差位置的像素值的一个邻域像素值。
将残差原型通过旋转变化,水平方向、垂直方向、对角线和反对角线方向各有2个不同的线性残差,即一共有8个一阶线性残差,如下。
此时,一阶非线性残差如下。
非线性残差综合了同类线性残差的统计特征,全面反映了隐写嵌入改动引起的图像相邻像素相关性变化情况,具有极高的应用价值。
基于线性、非线性残差的隐写分析模型
本隐写分析模型模拟了空域下线性和非线性残差特征的手工提取方式,模拟线性残差特征的方式见上一篇文章模型的信息。这里主要描述非线性残差特征的详细内容。
模型中非线性残差特征的设计
基于SRM的非线性残差统计特征更全面的特点,对空域下SRM HPFs获取的线性残差信息进行非线性变换,获得了非线性残差特征。
本文使用了一阶、二阶、三阶、SQUARE、EDGE3x3和EDGE5x5的这六类SRM高通滤波器(高通滤波器详细信息可见上一篇文章),它们的数量分别是8、4、8、2、4、4。这30个高通滤波器参与运算获得30个线性残差特征图。一阶、二阶、三阶的非线性残差特征图各有2个。SQUARE分为SQUARE3x3和SQUARE5x5,它通过变换生成了EDGE3x3和EDGE5x5。因此,SQUARE3x3和EDGE3x3本质上属于同一大类,一共有2个线性残差特征图,SQUARE5x5和EDGE5x5同理。因此,这两大类各产生2个非线性残差特征图。经统计获得对应的一共10个非线性残差特征图。和使用线性残差信息初始化卷积核的方式一样,也使用得到的非线性残差信息初始化卷积核,此时卷积核有40个通道,前30通道使用线性残差初始化,最后10通道使用非线性残差初始化。
模型中非线性残差特征的实现
当获取每一张图像的非线性残差信息时,首先获取它的线性残差信息,此方法上一篇文章已描述。记获取到的线性残差信息为Resi,它有三十个通道,每个通道特征即为一份线性残差特征信息。
获取到Resi后,将它的三十个通道切分开,即获得30个线性残差特征信息。在tensorflow框架下切分方法如下:
inputnum0, inputnum1, inputnum2, inputnum3, inputnum4, inputnum5, inputnum6, inputnum7, inputnum8, inputnum9, inputnum10, inputnum11, inputnum12, inputnum13, inputnum14, inputnum15, inputnum16, inputnum17, inputnum18, inputnum19, inputnum20, inputnum21, inputnum22, inputnum23, inputnum24, inputnum25, inputnum26, inputnum27, inputnum28, inputnum29 =tf.split(inputnum, 30, 1)
在这30个线性残差特征信息中,inputnum0至inputnum7、inputnum8至inputnum11、inputnum12至inputnum19、inputnum20至inputnum24、inputnum25至inputnum29分别是五大类线性残差信息,即一阶线性残差、二阶线性残差、三阶线性残差、SQUARE3x3+EDGE3x3、SQUARE5x5+EDGE5x5这五大类。
对每类残差特征信息进行非线性变换,即求得它们的最大最小值。以一阶线性残差这一类为例,代码如下:
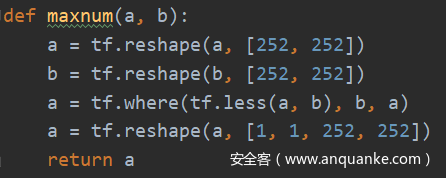
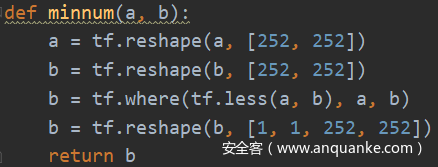
maxnum0 = maxnum(inputnum0, inputnum1)maxnum0 = maxnum(maxnum0, inputnum2)maxnum0 = maxnum(maxnum0, inputnum3)maxnum0 = maxnum(maxnum0, inputnum4)maxnum0 = maxnum(maxnum0, inputnum5)maxnum0 = maxnum(maxnum0, inputnum6)maxnum0 = maxnum(maxnum0, inputnum7)minnum0 = minnum(inputnum0, inputnum1)minnum0 = minnum(minnum0, inputnum2)minnum0 = minnum(minnum0, inputnum3)minnum0 = minnum(minnum0, inputnum4)minnum0 = minnum(minnum0, inputnum5)minnum0 = minnum(minnum0, inputnum6)minnum0 = minnum(minnum0, inputnum7)
这样得到的maxnum0、minnum0即为最大最小的一阶非线性残差信息。其中,maxnum和minnum函数分别定义如下:
隐写分析模型性能比较
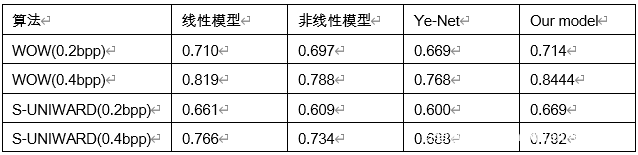
本文称仅模拟线性残差特征提取的隐写分析模型为‘线性模型’,仅模仿非线性残差特征提取的隐写分析模型为‘非线性模型’,同时模拟线性和非线性残差特征提取的隐写分析模型为‘our model’,实现的隐写分析实验如下表。
其中,表格中Ye-Net是一个有名的卷积神经网络隐写分析模型。
首先分析‘线性模型’和‘非线性模型’。在WOW的隐写分析检测中,‘非线性模型’的准确率低于‘线性模型’约2%,但在S-UNIWARD的隐写分析检测准确率低于约3%~%6。本文认为非线性残差特征粗糙地统计了每类线性残差特征的最大最小值,没有考虑每类中残差特征值在这一值域的分布特征,因此没有较全面地反映所有可能的隐写嵌入改动引起的图像相邻像素相关性变化,即没有充分发挥非线性残差特征的优势。但‘非线性模型’的准确率均高于CNN隐写分析网络Ye-Net,说明‘线性模型’具有良好的竞争性,能增强隐写信息的特征表达。
‘our model’对WOW和S-UNIWARD的隐写分析检测效果均好于‘线性模型’和‘非线性模型’。在嵌入率为0.2的WOW和S-UNIWARD隐写算法中,‘our model’的隐写分析准确率高于‘线性模型’和‘非线性模型’约0.3%到%6,效果不特别显著,对比高嵌入率隐写分析准确率可知,这主要是隐写过程中嵌入秘密信息过少造成的,说明本文设计新型线性非线性隐写分析模型仍然可行。







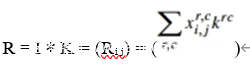


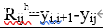
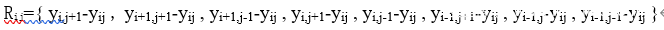
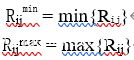








发表评论
您还未登录,请先登录。
登录