2019年9月,莫斯科市议会选举的选民被允许使用互联网投票系统。它的源代码已提供给公众测试。在本文中展示了对投票系统中实施的加密方案的两次成功攻击。两种攻击都发送给系统的开发人员,此后这两个问题均已修复。
该系统中使用的加密是ElGamal在有限域上的一种变体。在第一次攻击中,表明使用的密钥大小太小。将说明如何在几分钟之内使用容易获得的资源从公共密钥中检索私有密钥。
解决此问题并使用新系统进行测试后,发现新实现在语义上并不安全,将演示如何使用此新发现的安全漏洞来计算候选人的投票数。
0x01 Introduction
电子投票越来越多地用于具有不同系统的低风险投票选举。具有重要政治约束力的选举的情况更加鲜明。在这种情况下,一些国家已经完全禁止使用电子投票(例如,德国于2009年,荷兰于2008年或挪威于2013年),而其他国家则定期使用电子投票或组织实验越来越高风险的投票(瑞士,爱沙尼亚,加拿大)。
电子投票一词可以涵盖不同的情况,在这项工作中对互联网投票感兴趣,而不是在投票站进行的机器辅助投票。这就增加了难以保证在投票站更容易获得诸如身份验证或抗胁迫性之类属性的困难,在投票站中,官员可以检查身份证,选民可以去投票站隔离自己并自由选择。
但是,如果要保持简单并且没有高级加密工具(如零知识证明,等价明文证明,不经意传输等),则要使事情变得简单,就很难获得更多的基本属性,例如投票保密性和可验证性。
对于高风险的选举,人们不太接受的一个坏做法是让一些指定的专家研究产品的安全性,但其实际运作方式仍是选民的秘密。因此,在越来越多的情况下,组织将要求一种可以由独立专家审核的产品,并且为了获得更多反馈,可以组织带有相关漏洞赏金计划的公开测试。例如,最近在瑞士就是一个例子,瑞士是一个拥有悠久的互联网投票实验历史的国家。在这种情况下实际上发现了一个安全问题。
在俄罗斯,2019年9月8日是地方选举的一天,必须选举地方长官和地方议会代表。在莫斯科,在举行市议会(莫斯科杜马)选举时,决定测试使用互联网投票的方式。允许来自3个选举区(总共45个区)的选民进行注册,以使用互联网投票,而不是在投票站使用经典纸质投票。
本次选举使用的投票系统是专门设计的。由于缺乏专有名称,将其称为莫斯科互联网投票系统。它的部署是纽约市信息技术部的一项服务。7月该系统开放供公众测试。
2019年7月17日,系统的一些代码在线发布,组织者要求公众测试几种攻击情形。与之相关的一项赏金计划高达200万卢布(约30,000美元)。大多数信息都是俄语的,而且除了源代码外几乎没有任何系统描述(任何语言),这是在国际上对这一挑战的宣传不高的原因,甚至在电子投票社区中。
该系统的文献不多,但是从系统的源代码和简短描述,知道该系统使用了以太坊区块链和ElGamal加密。源代码中没有高级加密工具(例如,没有可验证的混合网络,尽管它们在现代系统中很常见)。
在一种攻击情形中,组织者发布了一个包含公钥和一些加密消息的挑战。如果在组织者透露私钥和原始消息之前的12小时(未来真正选举的持续时间)内将消息解密,则认为攻击成功。所有这些加密挑战(密钥和加密数据)都放在源代码的公共存储库中的特殊子目录中,该子目录称为加密密钥。
在本文中描述了此攻击情形下在系统上进行的两次攻击。第一次攻击使用这样一个事实,即密钥的大小非常小,以至于使用专门的软件,可以在不超过此任务允许的12小时的时间内计算离散对数并推断出私钥。此后修改了源代码。
第二次攻击是针对此新版本的攻击,它依赖于一个子组攻击,该攻击揭示了与原始消息有关的一点信息。在电子投票的情况下,这足以获得有关选民选择的大量信息,并且实际上,在莫斯科系统中,泄漏真的很严重。在修补了针对本文攻击的系统后,八月份,志愿者进行了几次公开测试。
在本文中,在描述了攻击之后将讨论通用协议,这是一种不断发展的目标,因为没有适当的规范, 没有明确的安全要求,除此之外,直到真正选举之前很晚才进行了深刻的改革。
对于这项工作,使用了以下有关莫斯科互联网投票系统的不同信息来源:
•公共源代码,这包括将在客户端运行的Javascript代码,在服务器端运行的PHP代码以及将以智能合约形式运行在以太坊区块链中的Solidity代码。
•媒体上发表的文章,有时会引用系统的设计者。这包括各种来源,对于在这种情况下使用互联网投票有不同的看法。认为其中某些来源不可靠。
•与设计师和记者进行私下讨论,以调查当前情况。
在下文中将引用不同版本的源代码。为了使术语更精确,给出了这些版本的确切修订版本号,对应于公共存储库中的git commit :
•“original”版本,即已发布并用于首次公开测试的版本:修订版d70986b2c4da。
•考虑到首次攻击的“modifified”版本:修订版1d4f348681e9。
•选举使用的“final”版本:修订版51aa4300aceb。
(https://github.com/moscow-technologies/blockchain-voting)
0x02 Attacks on the encryption scheme
A.攻击原始实现
在原始版本的源代码(rev d70986b2c4da)中,可以在smart-contracts/packages/crypto-lib/ src/子目录的elGamal.js和multiLevelEncryptor.js文件中找到加密方案。第一个文件包含ElGamal加密算法的经典版本,而第二个文件在此文件的基础上构建了一个“多级”变体,将在此进行描述,因为这是非标准构造。
首先重申经典ElGamal加密的符号。令G为由q阶g生成的循环群团。通过选择(秘密)解密密钥sk作为Zq中的随机整数来获得ElGamal密钥对,并且对应的(公共)加密密钥pk由pk = g^sk给出。
用Encg,pk(m)=(a,b)表示用公钥pk和生成器g对消息m∈G的ElGamal加密。这是一种随机加密,在Zq中随机均匀地选取一个整数r,然后将其加密为:
然后,使用对应于pk的秘密密钥sk的相应解密函数Decg,sk(a,b)给出:
通过依次对消息m和随后的连续ElGamal密文的a-part依次应用具有三个不同参数集的ElGamal加密,可以获得多级变体。在莫斯科系统中,共有3个等级。每个级别使用一个组Gi,它是有限域Fpi的乘法组,其中pi是安全素数。这里的一个重要说明是pi是不同的,从一组到另一组没有代数映射。在将Fp1的元素映射到Fp2之前,有必要将其元素提升为[1,p1-1]中的整数。仅当p2大于p1时,此映射才会丢失信息。同样,需要p3大于p2。这些条件确实在源代码中强制执行。
用g1,g2,g3表示3组G1,G2,G3的生成器。有3个ElGamal密钥对(sk1,pk1),(sk2,pk2),(sk3,pk3)用于选票的加密和解密。为了加密消息m∈G1,计算以下连续的ElGamal加密:
则密文为G1×G2×G2,3的四元组:
值a1和a2被遗忘,但是知道私钥sk1,sk2,sk相当于pk1,pk2,pk3,将可以通过以下解密过程从密文中恢复m:
不知道这种多级加密的目的。但是,显而易见的观察是,如果在G1,G2和G3中离散对数问题不难解决,则可以从公钥pki’推导出秘密密钥ski’ ,然后攻击者可以与秘钥的合法拥有者一样快地解密加密的消息。
在已发布的源代码中,素数pi少于256位。由这样小的素数定义的有限域中的离散对数是在90年代中期首次计算的:Weber,Denny和Zayer在1995-1996年进行了一系列计算,从215位到281位。那时,计算所需的计算资源相当大,并且要解决挑战所需的少于12小时的时间,解决3个离散对数问题以获取私钥并不容易。
20多年后,计算机变得更快,并且拥有更多的内存。此外,渐近最快的已知方法Number Field Sieve算法在90年代中期仍然是一种非常新的算法,并且从那时起已经开发了许多理论和实践上的优化方法。当前记录是以768位素数为模的计算。
已经尝试了以下软件产品,这些产品在素数字段中包含离散对数计算的完整实现:
请注意,Magma是专有软件,而其他是免费软件。实验首先在配备了4核Intel i5-4590处理器,3.3 GHz频率和16 GB RAM的典型个人计算机上进行。它运行标准的Debian发行版。SageMath内部使用GP / Pari 计算离散对数。在这台机器上,计算耗时超过12个小时,实际上必须在运行4天后将其停止。
根据GP / Pari文档,使用的算法是线性筛分指数演算方法。至于Magma,,该手册表明根据素数的算术属性,使用的算法可以是高斯整数筛或后备线性筛。测试的素数与高斯整数筛兼容。但是在线性代数步骤中,内存需求远远大于可用的16 GB。在具有192 GB RAM的64核服务器节点上再次开始了计算。
在这台机器上,Magma在不到24小时的时间内计算了130 GB的峰值内存使用量的离散对数。应该注意的是,Magma和SageMath都仅使用一个可用的计算核心,因此,即使使用了功能强大的机器,似乎也没有一种简单的方法可以使它们达到12小时的限制。
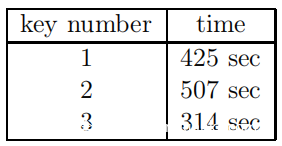
CADO-NFS是“数域筛选”的一种实现,用于质数域中的整数分解和离散对数(以及一些对质数域小范围扩展的实验支持)。最新的稳定版本2.3.0已有两年的历史,因此使用了开发版本,该版本在公共git存储库中提供。使用CADO-NFS,在标准个人计算机上,检索8月18日私钥的运行时间如下:
请注意,从一个密钥到另一个密钥的运行时间变化对于带有适中小素数的计算而言并不罕见。另外应该提到的是,在进行这项工作时,意识到开发版本对于这种规模的数字并不可靠:有时在称为“个人对数”或“下降”的最后一步中失败。上面给出的修订版本号对应于一个已解决这些问题的版本,因此CADO-NFS可以可靠地计算大约256位有限域中的离散对数。
CADO-NFS不包括离散对数的“前端计算”:由于生成器的阶次是质数的两倍,因此需要执行小的Pohlig-Hellman步长;类似地,由CADO-NFS计算的离散对数的底是任意的。因此,为了计算其中之一,该程序必须运行两次,一次针对生成器,一次针对公钥。
幸运的是,在Number Field Sieve算法中,可以在两个执行之间以相同的素数为模(这是LogJam攻击的基)共享计算的许多部分,并且CADO-NFS确实自动共享它们。上面给出的运行时间包括每个密钥的两次运行。为了完整性和可重复性,除了调用CADO-NFS之外,这还包括一些额外的模块化操作。
当然,对于真正的攻击,可以在3台并行计算机上同时计算三个私钥。实际上,多级ElGamal中涉及的链接与密钥无关,它仅在消息的加密/解密期间发生。
除了针对攻击的这种三倍立即并行性之外,CADO-NFS还具有一些并行性功能,因此具有更多内核的计算机可以减少单个密钥的时间。但是,当前的实现对此有一定的限制。例如,在用于测试Magma的同一台64核计算机上,私钥1仍需要160秒的时钟时间。
B.对修改版的攻击
在将第一次攻击发送给系统的开发人员并在几天后公开之后,公共源代码已被修改。密钥大小已增加到1024位,并且多级ElGamal已被删除并由单个ElGamal加密代替。
在原始版本中,所有相关组中的生成器都是有限域的完整乘法组的生成器,因此它们的阶次是质数的两倍。这样就暴露了由于子组攻击而导致消息中的某一信息泄漏的危险。这是一种旧技术,但是仍然存在频繁的攻击,特别是当实现忘记密钥验证步骤时。尽管在第一次攻击中没有朝这个方向努力,但明确提到它是一个弱点。因此,在修改版本中,生成器被选择为二次余数,因此具有素数阶。
但是发现实现的其他部分没有相应更改,因此仍然有可能受到攻击。
令p = 2q +1是用于定义组的1024位安全素数,其中q也是素数。令Qp为p的二次残基群;它有订单| Qp | =(p-1)/ 2 = q。所选择的生成器g属于Qp,因此,公钥pk也属于Qp,因为它像以前一样计算为pk = g^sk,其中sk是在Zq中随机选择的。
修改后的实现的问题在于,消息m可以是[1,q-1]中的任何整数,该整数自然映射到Fp的元素。为了语义安全(在Decision Diffie-Hellman假设下),消息m应该编码为g生成的Qp组的q个元素之一。在不必从二次残差组中选择m的情况下,Decisional Diffie-Hellman假设不成立,并且确实有可能构建有效的区分符,从而表明修改版本中的加密方案在语义上并不安全。
明确一点,如果消息m在映射到Fp之后变成二次残差,则对于加密算法的每种随机性选择,在所得密文Encg,pk(m)=(a,b)中,第二个分量b也为二次残基,如果g和m属于Qp,则在Fp中存在x和y,使得g = x^2和m = y^2:
同样,如果m不是二次余数,则b = pkr·m也不是二次余数。
可以通过计算b和p的Legendre符号来测试b的二次残差。得益于二次互易定律,类似于欧几里得算法的非常有效的算法可用。因此,仅从密文的知识就可以立即推断出相应的明文m是否属于Qp。大约一半的消息被映射到Qp。因此,泄漏了一点信息。
为了测试此攻击的有效性,检查了已发布的加密消息的b部分是否属于Qp。事实证明,十分之十是p的二次残基。这表明确实有一些明文在Qp中,而有些则不在Qp中。
C.关于加密在协议中的作用–攻破了什么?
与许多电子投票协议一样,加密方案用于对投票者的选择进行加密以形成加密选票。根据应该在选民的投票设备上运行的Javascript源代码(在名为voting-form的子目录下),推断出加密数据仅由该选择组成(不包含其他随机数或元数据) )。它采用称为“代理ID”的32位无符号整数的形式,该整数看起来是随机的。
代理ID与候选人真实姓名之间的链接是公共的,因为必须向选民展示选择的Javascript源代码必须包括它。
在加密方案的原始版本中,选举开始后,多级ElGamal的3个公钥必须公开,并且可以在几分钟内从中推导出解密密钥。然后,好像选民的选择在整个过程中都是明文。即使在接收这些选票的服务器上有很强的信任假设,即使是诚实的并且忘记了选民和选票之间的联系,仍然存在将其放入区块链以进行验证的问题。
由于选票(基本上)是明文形式的,部分结果在选举当天全天公开,这可能会对结果产生重大影响。实际上,在选举期间,宣布任何初步结果在俄罗斯是非法的。
第二次攻击不会提供完整的信息。加密的选票仅泄露了一点信息,即所选候选人是否具有代表二次残差的副身份证。由于副id似乎是随机选择的,没有特定的运算特性,因此对于F ∗ p的任何元素,它们都属于Qp的概率为二分之一。如果副ID只有几位,但具有32位整数,则可能会有一些偏差,根据标准数论启发法,情况并非如此。
那么,一个可能的攻击场景就是一个区域,其中两个候选人集中了大多数选票,其中一个在Qp中拥有副身份证,而另一人则没有。然后,通过加密的选票,通过计算勒让德符号,人们可以推断出选民的选择,除非选民为不太受欢迎的候选人投票。
因此,对于第一次攻击,此第二次攻击意味着投票保密性依赖于投票服务器中非常强的信任假设,并且部分结果在整个过程中都是泄漏的。
最初,似乎设计人员对第二次攻击的可行性持怀疑态度,并且他们否认这是威胁。但是在2019年8月28日,他们组织了最后一次公开测试,只有两个副ID。由于其中一个ID位于Qp中,而另一个ID不位于Qp中,因此它完全容易受到上述攻击。但是,尽管尚未修改公共源代码,但在测试过程中为志愿者提供的(最小化)JavaScript包含了针对第二次攻击的补丁。
0x03 Discussion
A.区块链在协议中的作用
1)区块链作为分布式账本
在协议中,加密的选票被发送到以太坊区块链并存储为交易,每选票一次交易。这样做的论点是电子投票中的一种典型说法,即为选民提供检查确实考虑到他们的选票的可能性。
选举结束时,再次通过区块链,还为选民提供了一种方法,可以将每个加密的选票与明文形式的对应选票相关联。目的是提供按预期的属性:如果有投票的客户要悄无声息地修改投票者的选择,则会检测到这一点。
在上面的快速描述中,隐式地假设,一旦选民检查完她的选票是否存在于区块链中,它将停留在选票中并计算在内。这也假设选民有足够的信息和工具来记录他们的选票和区块链中相应条目之间的链接,以便可以在选举后的几天(也许是几周或几个月)内进行检查。
在莫斯科大选中,使用了特定的,经过许可的以太坊区块链。因此,运行此区块链的节点无法重写分类帐本的历史记录,以便在选民检查后删除选票,因此要基于这样的假设,即足够的节点是诚实的。此外,不能保证对该特定区块链的访问持续很长时间,实际上在选举后组织者很快将其切断。
如果无法访问协议的规范,很难得出明确的结论,但是认为可验证性不如基于区块链的分类帐所希望的那样强大。
2)使用或不使用智能合约进行解密
在最初的实现中,选举结束时,使用了多层ElGamal的3个私钥来公开解密所有选票。该解密以Solidity编程语言实现,将作为智能合约的一部分由区块链的节点运行。这样做寻求的安全属性尚不清楚。有很多方法可以确保解密已正确完成,在ElGamal加密设置中,最明显的方法是包括简单的零知识证明。
在第一次攻击后修改的版本中,协议已更改,因此解密是在智能合约之外进行的。解密结果(即票数清楚)作为简单交易上传到区块链,无需计算。当然,此操作会在选举结束时进行,以计算计数。此外,私钥也存储在区块链中。这确实允许选民验证解密是正确的。
在真正用于高风险的选举之前几周,对协议进行如此大的更改绝对不是一个好习惯。但是,同样,如果没有适当的规范,很难推断出所有后果。信任假设在过程中是否发生了变化?这也使得人们有可能在智能合约中对解密进行编程只是原始设计的特殊性。
3)这是小密钥大小的原因吗?
原始代码包括许多检查,以确保用于定义多级ElGamal加密组的素数的大小足够小,以便它们可以容纳256位。这是采用与定义为2^256-1的常量SOLIDITY_MAX_INT进行比较的形式。实际上,它对应以太坊智能合约的Solidity编程语言本地支持的最大(无符号)整数类型。
与设计者的私人交流证实,删除智能合约代码的投票解密并相应更改协议的原因是由于缺乏时间在Solidity中实现多精度库,因此在增加密钥后就变得很有必要大小为1024位。
尽管最初为质数选择的位大小与Solidity本机支持的最大整数大小的一致性令人震惊,但很难确定这是错误的原因。但是可以推测并认为ElGamal的多级变体的目的是补偿这种公认的较小的密钥大小。
设计师可能希望通过使用三个连续的加密来提供更好的安全性,就像Triple-DES比DES强大得多一样。不幸的是,非对称密码的情况大不相同。使用256位密钥的另一个原因可能是椭圆曲线加密带来的安全性与有限域提供的安全性之间的混淆。
B.D日发生了什么
考虑到第二次攻击,9月6日(选举前两天)对公共源代码存储库进行了更新。在最终版本中,要加密的消息m在传递给ElGamal加密之前已平方,因此,实际上,加密的数据是二次余数。
选择用来定义该组的质数等于3模4。这具有以下结果:(-1)是Fp中的二次非残差,而Tonelli-Shanks模平方根算法最简单形式,即提高到幂(p +1)/ 4。
为了在解密后恢复原始消息,将执行模幂运算的平方根,并且符号选择基于ppm和m的相对大小(介于1和p-1之间的整数)。实际上,所有副身份都是加密为比p小得多的整数。
这接近在在发布第二次攻击时提出的修复程序,但不是在加密过程中进行额外的幂运算并进行廉价的解密,而是在此加密方法廉价且解密包括额外的幂运算。这是有道理的,因为解密可以在高端服务器上完成,而加密则在选民的设备(可能是智能手机)上进行。
因此,在9月8日,选举以不容易破解的加密程序进行。尽管即使对于中期安全性而言1024位是不够的,但要在不到12小时的挂钟时间内解决该大小的离散对数问题,当然是很困难的(不是说不可行)。利用当前的公共算法知识(以及基于现有记录计算的推断),数十亿个计算内核将不得不动员起来并进行协作,即使有大公司或政府机构的资源,这听起来也不可能。
根据组织者的说法,在三个地区,超过一万名莫斯科人使用了互联网投票系统。在一个区中,第一名候选人和第二名候选人的总和不到100票。回想起来,这证明了该实验的真正意义,因为系统中的欺诈风险直接意味着最终结果的风险。
在选举期间,可以通过Web界面访问区块链数据,并且其中存在加密的选票。最终,私钥也被发送到区块链以进行验证。但是几个小时后,对区块链的访问被切断了。幸运的是,Meduza在线报纸的分析师记录了一切,并提供了数据。他们还使用私钥对在区块链中找到的9810加密选票进行解密并发布。他们从这些数据中观察到的统计数据对选举的公平性提出了疑问,但是仅从已发布的数据中得出结论是不可能的。
在揭示了解密密钥之后,这种对区块链访问的减少看起来像是一种尝试减轻投票秘密的风险的尝试,同时仍然具有某种可验证性。这似乎并不令人信服:大选后不久,俄罗斯联邦中央选举委员会负责人Ella Pamfilova公开发表声明,明确表达了对该实验结果的关注,并且在未来几年内不应这样做扩展到整个国家。
C.在没有规范的情况下
莫斯科互联网投票系统的主要问题是:
•没有公共规范;
•在选举前匆忙进行的修改
在明确的规范中,希望找到有关在系统中起作用的每个实体的任务的更多详细信息。仅从源代码并不总是清楚应该由谁来运行代码的某些部分。还需要有关于安全声明和信任假设的清晰声明。
尽管设计师显然考虑了一些可验证性,因此使用了区块链,但他们当然也希望维护投票的保密性,因为在这种政治背景下,这始终是一项要求。但是,似乎对于接收(加密)投票的Web服务器的投票保密不是目标。此外,至少在最初,抗压性根本就不是问题。
不主张对任何投票系统都必须具有相对于投票服务器的抗压力和机密性。但这应该清楚地说明,以便验证系统使用情况的官员可以在知道风险的情况下做出决定。
具有清晰规范,具有良好陈述的信任假设和安全声明的理想过程与这次选举的组织方式非常不兼容。确实,尽管对协议进行轻微修改以解决问题当然是可行的,而不必从头开始进行安全分析,但设计师在选举前几周甚至几天所做的更改是如此重要,以至于如果此文档是公开的,他们将需要修改文档的页面。
实际上,似乎是在选举结束后不久就决定切断对区块链的访问,这是对一些关于隐私和强制性风险的负面报道的快速反应。他们决定以某种方式降低可验证性,以尝试保存其他属性。
0x04 Lessons learned and conclusion
从本文中学到的第一个教训并不奇怪,设计师在使用加密技术时应该非常小心。莫斯科系统的作者在决定使用的加密方案上犯了许多错误。实际上,即使在现在,从技术上讲,加密仍然很弱,原因有两个:
首先,对于中期安全性而言,1024位密钥太小,如果协议发生更改,以至于投票隐私依赖它,这将是不够的。而且质数的选择方式不是公开的,因此它可以包含一个陷门,使设计人员易于计算离散对数。
其次,现在实施的经典ElGamal不是IND-CCA2。根据协议的不同,这可能会导致轻微或破坏性的攻击。作为后者的一个示例,在一个协议中,该协议包括一个解密预言,该预言允许对不在投票箱中的任何密文进行解密(例如,出于审计目的),使用ElGamal的同态属性来得到所有的选票解密。
第二个教训是,使用区块链不足以保证完全透明。电子投票文献中有各种可验证性的概念,设计人员必须在精确的信任假设下清楚地说明他们拥有哪种属性。在使用许可的区块链时,必须更加仔细地做出这些信任假设,在这种情况下,可能专门选择运行区块链的节点进行选举,并且可以随时切断对区块链的访问。


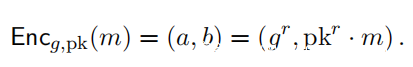
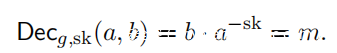
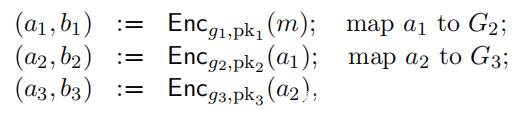
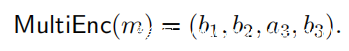
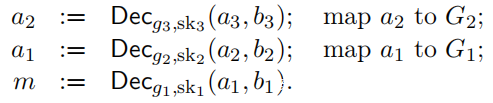

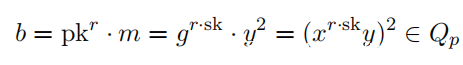







发表评论
您还未登录,请先登录。
登录