前言
zer0pts CTF 2020中有4道Crypto方向的题目,题目整体难度适中,在这里对这4道题目进行一下分析。
dirty laundry
题目描述:
Do you wanna air my dirty laundry?
题目附件:
dirtylaundry.zip
审计代码,可以发现本题是将Paillier Cryptosystem和Shamir’s Secret Sharing结合在了一起进行考察,题目的基本流程如下:
1. 首先生成一个1024位的强素数PRIME。
2. 使用PRIME的低256位做为PRNG256的种子,该PRNG会产生256位的输出,后面会用该PRNG来产生伪随机数。
3. 使用了一个(5, 3)Shamir门限,其多项式为f(x) ≡ a * x^2 + b * x + flag (mod PRIME),其中flag即为该门限的secret,a、b为GF(PRIME)下的两个随机数。
4. 将(f(1) + noise1)、(f(2) + noise2)、...、(f(5) + noise5)的值使用Paillier进行加密(每次加密时重新生成公、私钥),并将加密结果c1到c5和每次加密时使用的公钥(n1, g1)到(n5, g5)提供给选手,其中noise1到noise5、进行密钥生成时p和g用到的随机数以及加密时使用的随机数r均为PRNG256生成的伪随机数。
观察发现,每次在paillier_enc函数中生成密钥时,g是通过如下方式产生的:
g = (1 + prng.rand() * n) % n**2
这里的prng.rand()最大为256比特,n约为1536比特,因此(1 + prng.rand() n)约为256 + 1536 = 1792比特,而n**2约为1536 2 = 3072比特,因此这里的% n**2这一运算实际上没起着作用,由于我们已知(n1, g1)到(n5, g5),因此可以通过prng.rand() = (g - 1)/n计算出这5次prng.rand()的值。
我们知道这里PRNG256生成随机数的运算过程是可以逆回去的,因此我们可以借助其中一次的prng.rand()的值来反推出seed(即PRIME的低256位),既而得到所有prng.rand()的值。以`output
以output.txt中的(n1, g1)为例,我们有prng.rand()1 = (g1 - 1)/n1,审计代码可知这里的prng.rand()1是第二次调用,因此我们执行两次逆操作后,此时的seed值即为我们本题需要获取的seed值,计算脚本如下:
class PRNG256(object):
def __init__(self, seed):
self.mask = (1 << 256) - 1
self.seed = seed & self.mask
def _pick(self):
b = ((self.seed>>0)^(self.seed>>2)^(self.seed>>5)^(self.seed>>10)^1)&1
self.seed = ((self.seed>>1)|(b<<255)) & self.mask
return b
def rand(self):
x = 0
for i in range(256):
x = (x << 1) | self._pick()
return x
# 逆过程
def reverse_rand(self):
seed = self.seed
for _ in range(256):
b = ((seed>>255) ^ (seed>>1) ^ (seed>>4) ^ (seed>>9) ^ 1) & 1
seed = ((seed << 1) | b) & self.mask
self.seed = seed
n, g = [1341233826702376842498119940039016826282055747303464974435594326637538907180149241566365225911074218597539880291426265503244204409536388336349105099303221252199164187921036400118788488925884552440483653638244202969641876448593915624469362160298646189903056069767976491733960779483023305191435635289734365528710722401088230332490023131911734288011232016872906051832164035804891447455672110954242647111735228814935698789659541198379357658233047482430645842400366769, 26674131724614738833784434076708623929346303545393320399944409878863187402150503055207795853307211144249179748395076848334742855586049336411971031238044174387954252693537728148985955948048292029557791508049506146642880016520533230306989498523300220064692662847160710441255197572391506435448482713046019266895261344521636514739951705743608587218033949609867770113753539973249063631220635085754002655371345431327359674264770777710263422098079037291585196293197114766337658570276078577504309446984989309950901135119579313915133962619448102748]
out = (g - 1) / n
state = int(bin(out)[2:].zfill(256)[::-1], 2)
x = PRNG256(state)
x.reverse_rand()
x.reverse_rand()
seed = x.seed
print seed
执行脚本即可得到本题PRNG256的seed为:
60702825763651781569208648502945521408055748350006223555916359844074217637833
拿到seed后,本题中所有prng.rand()的值我们就都知道了,那么接下来我们的任务就是想办法对Paillier加密后的密文进行解密,来拿到(f(i) + noise_i)的值,继而拿到f(i)的值了。
观察发现,每次在paillier_enc函数中进行Paillier加密时,密文c是通过如下方式产生的:
c = pow(g, m, n**2) * pow(prng.rand(), n, n**2) % n**2
其中pow(prng.rand(), n, n**2)的值我们是可以知道的,因此我们这里可以通过如下方式计算出pow(g, m, n**2)的值(设pow(prng.rand(), n, n**2)的值为res):
pow(g, m, n**2) = (c * inverse(pow(prng.rand(), n, n**2), n**2)) % n**2
= (c * inverse(res, n**2)) % n**2
根据二项式定理,有如下表达式成立:
其中最右边的两项都可以写成n的k次方的形式,因此我们有如下表达式成立:
此时我们的pow(g, m, n**2)的表达式可以改写为:
pow(g, m, n**2) = pow((1 + prng.rand() * n) % n**2, m, n**2)
= pow(1 + prng.rand() * n, m, n**2)
= (1 + prng.rand() * n * m) % n**2
由于prng.rand()约为256比特,n约为1536比特,m不超过1024比特,而n**2约为3072比特,因此(1 + prng.rand() * n * m)恒小于n**2的值,因此该表达式实际上为:
pow(g, m, n**2) = (1 + prng.rand() * n * m)
至此我们共得到了pow(g, m, n**2)的两种表达形式,因此我们有:
(c * inverse(res, n**2)) % n**2 == 1 + prng.rand() * n * m
移项得:
(c * inverse(res, n**2)) % n**2 - 1 == prng.rand() * n * m
等式两边加m,得:
(c * inverse(res, n**2)) % n**2 - 1 + m = prng.rand() * n * m + m
= (prng.rand() * n + 1) * m
= (g * m)
移项得:
(c * inverse(res, n**2)) % n**2 - 1 == m * (g - 1)
此时我们即可恢复出m:
m = ((c * inverse(res, n**2)) % n**2 - 1) / (g - 1)
因为m = f + noise,而noise我们也是知道的,因此此时用m减去noise即可得到f。整理一下上述推导过程,我们可以写出恢复出f(1)到f(5)的值的脚本如下:
from Crypto.Util.number import *
pubkey = [[1341233826702376842498119940039016826282055747303464974435594326637538907180149241566365225911074218597539880291426265503244204409536388336349105099303221252199164187921036400118788488925884552440483653638244202969641876448593915624469362160298646189903056069767976491733960779483023305191435635289734365528710722401088230332490023131911734288011232016872906051832164035804891447455672110954242647111735228814935698789659541198379357658233047482430645842400366769, 26674131724614738833784434076708623929346303545393320399944409878863187402150503055207795853307211144249179748395076848334742855586049336411971031238044174387954252693537728148985955948048292029557791508049506146642880016520533230306989498523300220064692662847160710441255197572391506435448482713046019266895261344521636514739951705743608587218033949609867770113753539973249063631220635085754002655371345431327359674264770777710263422098079037291585196293197114766337658570276078577504309446984989309950901135119579313915133962619448102748], [1411836429669183892966134560305538366838547135114531535251720851922638607907850507674940852917802242615202155607148892358461384679202044548831141295353829571829695255020484687938869019916289932148352179781631904110271902114010910086393396910500275240681423526254331492385949217178047157696773667958133033180038804263460584550022281663780195927924119675790311322672399731902027722031296853164002026620552741589967849779933976523556743919696732887883645621044361611, 54901986783642835051699889113428335659585153809842942356885004842920465421336706391742814742564346205356241657334450930082155461145433648171896778260206136182255774717095790534292114459150791413586339545764791219429615253607065582132297246948860985575596282841990693455389149847062253133706015420405086059551754437445312366999921584484205222674268615179520174172834649126131935196501454388399695961162329114143523185659562031324488650262065740579199795214468943489727171700351304387397461071307646615194578618714043441377328663670751933627], [1827670639023479057974423662769264575893916686880865506873460556631343496594640149665454545389837639322275346518374263849034235979447405363606817187890637783196194162726024155794431981524906947485134171466324929779048499566048313669091401079263506127226379009753084566863868890271238236467261185095363669354791741608878314575987029663948818461252180763032199904220494918133642971421746749038691538192915859604276912102975568194119467980419612286906176868952703619, 141955627685405861596265155634043580262274251775483613944451161608579951914157317215316282492132012795129761525653914539354069858559035449093879514616280531615371142125208924414389214738475566668885506757054698120214732427844927492109681218414883961942239601431792698791724207705264637074459890882510377535948407156226101316457666689930453121343643609559536469767469803312169661110669941502466830780526471703979445391121676012137033701185329849968518454602730837677935298633914797575550202371889703865031673251813095889426000075905120210715], [1402052496936016320097183149388969226815975944499402219852856803114088852450193317864886134127265736138410526536722880486066577543930136034727844243512981614084924117627899623040044660188020312540158405739267327536264551679882312483493710047604544613918162585552941665913115010517121759370648692761286982491236666306877105976920137441035714264352280173247224313429635552985171274872512067599818448065403462190853902179488909659352339753894521914217223448955215971, 86436796561750399172835178406595458158200152808363576725949152209752050457844658406574932376510960241857243310231191629391788175840467781934160642603459961684570827889722817126673212897198457329009359718685889481495826330541120466944045405490044949949259866864077324005529448874478602844692164951174440203087657096219194318354305991767616656455848089449159017933275879827733328877162500978230626795632715808168172022720272496925901610663582044355831900584113960342572153829531696471382379336709069115911649499884361699625754418888357105356], [1342704677106999319938700388688741153377785166648218447242877900112547844266669406514804811924511017558918915960330401218483170328967889513789896923310776509048521832125539811902549091395153161067069971385687776610710438852173147435486069694433486331195576027716222479219032032167578074212853391036064686760331515843088926026790746958731708142341497399752153088465594599246790180097507576747721603670126927119225609501504821203851575717696464442894256866979152071, 151778423244836361358618726678490961359665141861531434745037765026759553125937345447572403824004985824284188179016742237419300096576909738404031925822083587101759301624897645367726786635718018753092807084873240915940763159043557284908261185169254084475196021977237239622460403373815939034200532293365581548664725892312716054043939540402460543140481578956351181169010805594314620139932866466533726652277935117332880706565744981667712583109377942817662191762058437395347618376144282145949244368040832594427185427142218601311894439404196869044]]
shares = [[1, 597508787369395694379078055274758557631538862739941784216641187447047696613646680523204534254585433553841883904815873020522119769161150848487658944289025139852884425534715254212765760070437058597554314741974198161950731308938774064571532399460855957695621714795771549456243813779399463109411846725520743344118554521413815793297768851076100135443002760221642947948812785225122631701884241216019284262219988306790748365483241216049579680655534490056279281295122379176443966669667315043992274193717298501474638381448820981658485993472350525815696097401765948865514729845467484551526100202532018343011967560856014086051860031235536215643818290727062383335942089683311730283931932548912461126311217820002459492022071267001562804194559301166310110244724819006466684456151803974731484616982434451280906366032894303395363863415992620820995729046300233942195095878917887892047030748729267329243516360791348477702146680442138382721731], [2, 1456602020473336436595302182756958090511415476510657696986700623481719785551149148046222482541285365312188959543693509514194665154201380523065476755444520574235515226702501340621170242202481024616882142010693536315240074931107987736512086290237614373546387137118763177589626855206838418103751404170044959913691735814429141324338320985853997370723970242452295801714270370307506226450063833723978620621565509156414542500828358085837989711050634637181122088180962097398190523961973415973551114076986713383243786853784427170667899647985426058777600468130304251574650780445218699779580427275505399994170596637813422179447545139427789051628741760457519163521253124217051884027796849542531386743511788474207049545545002209680929220223136064442178057025754413867781284144371821327271523387818972046823739716532656252490038504917848103009173556160906958786293914926056507083575731302212603218169279706378356509037364037831069878231086], [3, 1595390928798835569336924563570335102923880736692143989367168050283822219400199743337809496383236309872055902908859973435410009867512480962418933647220942557496021772016027755153856780432756247783750165029188435931829475752098685139218491512524939261083097196175538068246302620283880442794354650203913256502298415299185414984420565985768541932846631373242689036582178180151029187744659165675733768586790929935335022733816827888717408760672442814312920814112098749134708381258920239270611481275188904733904484814532961896311957117153388398557892281039130937627251977203045005113457955326984992365109238884156875118258875576742912093629961904108637328565523791833431848861487780279931219592300441525537266970002720517825091950356133381996157142667046040400474609347986971206237389511449743320732065481903260813584781835955382208803634275373602785992176618584713593998708722680023507255977968510697362982348044089009664597010849], [4, 1011012847725577745336080393532189501492336190558468303901251128666948418862933107036802327706950463653743889588322849131239222018844807849320331335500253801822404870042943180018988070672118930708294758392176800835465940314497189212667345256623160148381248676718065742459754530766291525548914975338009832256832712589706835806517309607232698495103676951407256990497727674074485975124944372384103938197756270712242538878327377737064117888518506218677244903776303353809628478075251845418928422454505051034628606854452823018144040158582352384256981850775768889499743760124313790601039804655287368427678715298719610014768027055861100647302291703640051847379108339724116217620803865940790490720181318014407063347236752588796661376810081172579531972899972207972694482013181432385593628852052754597961311854114120889315842451116669964549895840227042765846799089720825799247881359370434521814841837587026380076995924399761319705723220], [5, 585069911394639305069783453652980853778745872799905806085352980735658699442233349825102728267563130252863283620016490723644364840781783036228871276919495247201207769697803633760636387168623971368425694237096294184568991213677440659398241600565247753979592046970818227704368395870777535026523567976874952173624307944192305292867662966386645876919788206043645183603762002422420998136405555517112532618282483706131862387809257609229574812285296154253501278056085465591743515177435365781927790199047842732048344042345351145298190659111295473008507446985055866290274758068271147032318530780490684852153963206087326840116434394159695925404604438964668680275485416592324577630006500633520246499405212932824588562414909326852417065336364436077691987208909857190371325101826958691831214195954288881703669647778463778679987622877010187433236808312183932607053247793338457198918138891876330549197934696966944916096701567755521275990739]]
class PRNG256(object):
def __init__(self, seed):
self.mask = (1 << 256) - 1
self.seed = seed & self.mask
def _pick(self):
b = ((self.seed>>0)^(self.seed>>2)^(self.seed>>5)^(self.seed>>10)^1)&1
self.seed = ((self.seed>>1)|(b<<255)) & self.mask
return b
def rand(self):
x = 0
for i in range(256):
x = (x << 1) | self._pick()
return x
seed = 60702825763651781569208648502945521408055748350006223555916359844074217637833
x = PRNG256(seed)
flist = []
for i in range(5):
n, g = pubkey[i]
_, c = shares[i]
noise = x.rand()
_ = x.rand()
r = x.rand()
res = pow(r, n, n**2)
m = ((c * inverse(res, n**2)) % n**2 - 1) / (g - 1)
f = m - noise
flist.append(f)
for i in range(5):
print flist[i]
执行代码即可得到f(1)到f(5)的值依次如下:
2435914717685014138649749236252905405722244694217680922681036751164195655875157002256026859740475344129647207688117380843197222261605411632547300570215065622883430626991992801471988987720414826443330294552571798697565316320513515219156268420705277864644965968187930985261740670894980651003125565782603329258
20683250518964539499743236211758446075493369914357947433664010111557386690597414223589079715811588368007495910608948249861895863617100579847236455467224717178523894669994061392037830812205180324552823269953637928728164642186434056742879218600096103755434917880264040400650648342866168452385107624119439408338
54742007403838576083280460926516622009313375660420799532948920081179573104166771663999158568213339071633546108762492607056095924066485504644067464691028954666921392129006205771697546186615831688090037710332007896626736848265236140709460769552186985903606415208499524690638870733997541149897334701132413864757
104612185372307123889261423380527433207182261932406237220535766660030754896583229323486263416945727455007797802148750452425797403609760186023040328241627778088075923004028425940451135110952368917054973615687681702393281934556919767118900921276977924309159457952894383855226407844289098743539806796821526698515
29708217301991320530581690195693774548993971219288304983622128711255491646232601302092149732307102700626739970578885493492329522432347723561395539134342684442494209630846087330262818306752864785395128006191227634540543362715161482433791492073571875506211859005180660302516586880061144931959870897186694406563
拿到f(1)到f(5)的值之后,根据(5, 3)Shamir门限的特点,如果我们能知道f(1)到f(5)这5个多项式的值中任意3个的值,我们就可以恢复出flag了,但是本题还有一点不同之处在于本题采用的并不是普通多项式而是模多项式,因此我们还得先把模数PRIME恢复出来才能再用Shamir密钥共享算法的方法来恢复flag。
由于我们已知f(x)的表达式为f(x) ≡ a * x^2 + b * x + flag (mod PRIME),因此我们有如下表达式:
f(1) ≡ a + b + flag (mod PRIME)
f(2) ≡ 4*a + 2*b + flag (mod PRIME)
f(3) ≡ 9*a + 3*b + flag (mod PRIME)
f(4) ≡ 16*a + 4*b + flag (mod PRIME)
f(5) ≡ 25*a + 5*b + flag (mod PRIME)
此时我们可以构造出如下表达式:
f(3) - 2*f(2) + f(1) ≡ 2a (mod PRIME)
f(4) - 2*f(3) + f(2) ≡ 2a (mod PRIME)
f(5) - 2*f(4) + f(3) ≡ 2a (mod PRIME)
用2式减1式、3式减2式可得:
f(4) - 2*f(3) + f(2) - (f(3) - 2*f(2) + f(1)) ≡ 0 (mod PRIME)
f(5) - 2*f(4) + f(3) - (f(4) - 2*f(3) + f(2)) ≡ 0 (mod PRIME)
即:
f(4) - 3*f(3) + 3*f(2) - f(1) ≡ 0 (mod PRIME)
f(5) - 3*f(4) + 3*f(3) - f(2) ≡ 0 (mod PRIME)
将同余式写成等式,即:
f(4) - 3*f(3) + 3*f(2) - f(1) = k * PRIME
f(5) - 3*f(4) + 3*f(3) - f(2) = g * PRIME
这样一来,我们就可以采用求最大公约数的方法来尝试恢复出PRIME:
PRIME = gcd(k * PRIME, g * PRIME)
写出脚本如下:
from Crypto.Util.number import *
from gmpy2 import *
f1 = 2435914717685014138649749236252905405722244694217680922681036751164195655875157002256026859740475344129647207688117380843197222261605411632547300570215065622883430626991992801471988987720414826443330294552571798697565316320513515219156268420705277864644965968187930985261740670894980651003125565782603329258
f2 = 20683250518964539499743236211758446075493369914357947433664010111557386690597414223589079715811588368007495910608948249861895863617100579847236455467224717178523894669994061392037830812205180324552823269953637928728164642186434056742879218600096103755434917880264040400650648342866168452385107624119439408338
f3 = 54742007403838576083280460926516622009313375660420799532948920081179573104166771663999158568213339071633546108762492607056095924066485504644067464691028954666921392129006205771697546186615831688090037710332007896626736848265236140709460769552186985903606415208499524690638870733997541149897334701132413864757
f4 = 104612185372307123889261423380527433207182261932406237220535766660030754896583229323486263416945727455007797802148750452425797403609760186023040328241627778088075923004028425940451135110952368917054973615687681702393281934556919767118900921276977924309159457952894383855226407844289098743539806796821526698515
f5 = 29708217301991320530581690195693774548993971219288304983622128711255491646232601302092149732307102700626739970578885493492329522432347723561395539134342684442494209630846087330262818306752864785395128006191227634540543362715161482433791492073571875506211859005180660302516586880061144931959870897186694406563
kPRIME = f4 - 3*f3 + 3*f2 - f1
gPRIME = f5 - 3*f4 + 3*f3 - f2
PRIME = gcd(kPRIME, gPRIME)
执行脚本即可得到结果为:
140585567122378862387104433378097105120106057511025955512802421136855440421614185899958244529701650817503511020188836292478670779814576900422759506984678502999493277664214634568035779278461927226052502979829431711487256538346323453537408181700897043465882187108267957591896672793679696301352653014000083503049
该数确实是一个1024位的素数,那么我们这里的恢复可以认为是没有问题的,有了PRIME之后,我们只需依次恢复出多项式的系数即可,其中常数项即为flag:
from Crypto.Util.number import *
f1 = 2435914717685014138649749236252905405722244694217680922681036751164195655875157002256026859740475344129647207688117380843197222261605411632547300570215065622883430626991992801471988987720414826443330294552571798697565316320513515219156268420705277864644965968187930985261740670894980651003125565782603329258
f2 = 20683250518964539499743236211758446075493369914357947433664010111557386690597414223589079715811588368007495910608948249861895863617100579847236455467224717178523894669994061392037830812205180324552823269953637928728164642186434056742879218600096103755434917880264040400650648342866168452385107624119439408338
f3 = 54742007403838576083280460926516622009313375660420799532948920081179573104166771663999158568213339071633546108762492607056095924066485504644067464691028954666921392129006205771697546186615831688090037710332007896626736848265236140709460769552186985903606415208499524690638870733997541149897334701132413864757
f4 = 104612185372307123889261423380527433207182261932406237220535766660030754896583229323486263416945727455007797802148750452425797403609760186023040328241627778088075923004028425940451135110952368917054973615687681702393281934556919767118900921276977924309159457952894383855226407844289098743539806796821526698515
f5 = 29708217301991320530581690195693774548993971219288304983622128711255491646232601302092149732307102700626739970578885493492329522432347723561395539134342684442494209630846087330262818306752864785395128006191227634540543362715161482433791492073571875506211859005180660302516586880061144931959870897186694406563
PRIME = 140585567122378862387104433378097105120106057511025955512802421136855440421614185899958244529701650817503511020188836292478670779814576900422759506984678502999493277664214634568035779278461927226052502979829431711487256538346323453537408181700897043465882187108267957591896672793679696301352653014000083503049
a = ((f3 - 2*f2 + f1) * inverse(2, PRIME) % PRIME)
b = (f2 - f1 - 3*a) % PRIME
flag = (f1 - a -b) % PRIME
print long_to_bytes(flag)
执行代码即可得到flag:
zer0pts{excellent_w0rk!y0u_are_a_master_0f_crypt0!!!}
diysig
题目描述:
I made a cipher-signature system by myself.
nc 18.179.178.246 3001
题目附件:
diysig.zip
nc到服务器看一下,可以发现服务器提供了3个功能:
[1] Encrypt and Sign //用户输入msg,返回ENC和SIG
[2] Verify Encrypted Mesasge //用户输入ENC和SIG,服务器判断用户输入是否合法
[3] Public Key Disclosure //打印公钥(N, E)
任意一个功能执行一次后,与服务器的连接就切断了,因此本题应该是参数固定的题,审计一下server.py文件和diysig文件,可以发现本题的公钥是一直不变的,即功能3的打印结果是一直不变的。在功能1我们输入msg后,其ENC是对msg使用RSA加密得到的,其SIG是对msg使用一个自定义哈希函数得到的,ENC和SIG的生成过程中都没有引入随机数,即在功能1中输入同样的msg得到的结果也是一直不变的。本题还提供给了选手一个chall.txt文件,该给了我们作者某一次使用功能1时得到的ENC和SIG,我们的任务就是恢复出该次作者输入的msg。
观察功能2,可以发现当我们输入的ENC和SIG不合法时,服务器会打印出我们输入的ENC对应的正确的SIG,审计生成SIG的哈希函数,可以发现该哈希函数是将msg做了一系列运算,其中最后一步运算(Stage 3)如下:
H = H | 1 if m & 1 else H & 0xfffffffe
可以看到当m为奇数时,H也为奇数;当m为偶数时,H也为偶数,即m和H的奇偶性是一致的,因此当我们使用功能2输入一个不合法的ENC和SIG后,服务器会泄露SIG的值,我们可以借此来获得SIG的奇偶性,也就意味着我们知道了msg的奇偶性,即msg的最后一比特可以泄露出来,这样功能2就相当于变成了一个标准的RSA LSB oracle,我们可以输入任意密文,然后获得明文的最后一比特(关于RSA LSB attack可以参考这里),因此我们可以写出exp如下:
import decimal
from pwn import *
from Crypto.Util.number import *
ct = 0x3cfa0e6ea76e899f86f9a8b50fd6e76731ca5528d59f074491ef7a6271513b2f202f4777f48a349944746e97b9e8a4521a52c86ef20e9ea354c0261ed7d73fc4ce5002c45e7b0481bb8cbe6ce1f9ef8228351dd7daa13ccc1e3febd11e8df1a99303fd2a2f789772f64cbdb847d6544393e53eee20f3076d6cdb484094ceb5c1
n = 0x6d70b5a586fcc4135f0c590e470c8d6758ce47ce88263ff4d4cf49163457c71e944e9da2b20c2ccb0936360f12c07df7e7e80cd1f38f2c449aad8adaa5c6e3d51f15878f456ceee4f61547302960d9d6a5bdfad136ed0eb7691358d36ae93aeb300c260e512faefe5cc0f41c546b959082b4714f05339621b225608da849c30f
e = 0x10001
enc_of_2 = pow(2, e, n)
def oracle(ct):
r = remote('18.179.178.246', 3001)
r.sendline('2')
_ = r.recvuntil('ENC : ')
r.sendline(hex(ct)[2:])
_ = r.recvuntil('SIG : ')
r.sendline('00000000')
_ = r.recvuntil('!= ')
res = int(r.recvline().strip(), 16)
r.close()
return res & 1
def partial(ct, n):
k = n.bit_length()
decimal.getcontext().prec = k
lo = decimal.Decimal(0)
hi = decimal.Decimal(n)
for i in range(k):
possible_pt = (lo + hi) / 2
if not oracle(ct):
hi = possible_pt
else:
lo = possible_pt
ct = (ct * enc_of_2) % n
return int(hi)
msg = partial((ct * enc_of_2) % n, n)
print long_to_bytes(msg)
执行exp即可恢复出flag:
zer0pts{n3v3r_r3v34l_7h3_LSB}
ROR
题目描述:
LOL
题目附件:
ROR.zip
审计一下代码,可以发现程序循环m.bit_length次(m即int.from_bytes(flag, byteorder=’big’)),每次打印pow(ror(m, i, m.bit_length()), e, N)的值,然后将结果提供给选手,要求选手恢复出m,其中ror为一个自定义函数:
ror = lambda x, l, b: (x >> l) | ((x & ((1<<l)-1)) << (b-l))
不难看出该函数实际上就是一个循环右移函数,即本题中是依次对m的每个比特进行RSA加密,这里RSA加密使用的n和e没有直接给出,但是给出了n和e的生成函数:
N = 1
for base in [2, 3, 7]:
N *= pow(base, random.randint(123, 456))
e = random.randint(271828, 314159)
可以看出N可以表示为(2^x) * (3^y) * (7^z),根据实数乘法的奇偶性规律:
奇 * 奇 = 奇
偶 * 偶 = 偶
奇 * 偶 = 奇
我们可知N恒为偶数,同时根据:
当A > B时:
若B为偶数,A % B的奇偶性同A的奇偶性一致
若B为奇数,A % B的奇偶性同A的奇偶性相反
当A < B时:
A % B的奇偶性与A一致
可知此时pow(m, e, n)的奇偶性和m的奇偶性一致,因此我们拿到的结果当中每一行结果的最后1比特即为m的最后1比特,因此我们可以写出solver如下:
from Crypto.Util.number import *
f = open('chall.txt', 'rb').read()
data = f.split('\n')[:-1]
m = ''
for i in data:
m += str(int(i) & 1)
print long_to_bytes(int(m[::-1], 2))
执行代码即可得到flag:
zer0pts{0h_1t_l34ks_th3_l34st_s1gn1f1c4nt_b1t}
nibelung
题目描述:
nc 18.179.178.246 3002
题目附件:
nibelung.zip
审计一下源码,可知本题使用的FiniteGeneralLinearGroup类实际上是一个有限域上的矩阵乘法类,设X是明文矩阵,U为密钥矩阵,Y为密文矩阵,则其加解密算法为:
Y = U * X * U**-1
X = U**-1 * Y * U
其中明文矩阵是通过bytes2gl函数生成:
def bytes2gl(b, n, p=None):
assert len(b) <= n * n
X = FiniteGeneralLinearGroup(n, p)
padlen = n * n - len(b)
b = bytes([padlen]) * padlen + b
for i in range(n):
for j in range(n):
X.set_at((j, i), b[i*n + j])
return X
即先在明文字符串msg的最前面padding上n*n - len(msg)个bytes([n*n - len(msg)])这一字节,然后再将每个字节转化成整数按列优先顺序依次存入n行n列的矩阵中,我们nc到本题提供的服务器上,服务器会将flag的密文矩阵和生成密钥矩阵时使用的素数p打印给选手,flag的密文矩阵为6*6矩阵,因此可知我们本题中的n为6,除了打印参数以外本题服务器端的程序主要提供了两个功能:
1. 加密功能:用户以base64形式输入明文字符串,服务器返回加密后的密文矩阵
2. 解密功能:用户以base64形式输入密文字符串,服务器返回解密后的明文矩阵
既然服务器端直接提供了解密功能,那我们直接将flag的密文矩阵送进解密功能当中就可以了吗?答案并不是,观察可知我们输入的字符串都是按一个字节一个字节去理解的,每个字节的范围是0x0到0x255,即我们输入的矩阵必须其中每个元素都不超过255,这样当我们输入一个长度为36的字符串时才会被解析成一个6*6的矩阵拿去计算,而我们本题中的密文矩阵,其每一个元素都约为512比特,原原大于255的范围,因此没办法直接送进解密功能拿去解密。
既然没办法直接解密,我们可以想办法拆分密文矩阵,如果我们可以把密文矩阵写成如下形式:
Y = a0 * Y0 + a1 * Y1 + ... + an * Yn
其中a_i为常数项,Y_i为所有元素均不超过255的6*6子矩阵,这样我们就可以将Y1到Yn依次送进服务器端的解密功能进行解密,从而拿到X1到Xn,此时有:
X = U**-1 * Y * U
= U**-1 * (a0 * Y0 + a1 * Y1 + ... + an * Yn) * U
= (U**-1 * a0 * Y0 * U) + (U**-1 * a1 * Y1 * U) + ... + (U**-1 * an * Yn * U)
= (U**-1 * a0 * U * X0 * U**-1 * U) + (U**-1 * a1 * U * X1 * U**-1 * U) + ... + (U**-1 * an * U * Xn * U**-1 * U)
= a0 * X0 + a1 * X1 + ... + an * Xn
这样一来我们就可以拿到X,继而得到flag,那么接下来我们就是想办法将密文矩阵Y拆成这种形式,一种可行的拆法可以表示如下:
Y = a_(0,0) * Y_(0,0) + a_(0,1) * Y_(0,1) + ... + a_(n,n) * Y_(n,n)
其中a(i,j)表示Y中坐标为(i,j)处的元素值,Y(i,j)表示坐标(i,j)处元素值为1、其余位置元素值均为0的矩阵,这样既可达成我们的目标,我们将上述推导过程写成代码形式如下:
#!/usr/bin/env/ python3
from pwn import *
from base64 import *
from Crypto.Util.number import *
from fglg import FiniteGeneralLinearGroup
def list2FGLG(n, p, l):
X = FiniteGeneralLinearGroup(n, p)
for i in range(n):
for j in range(n):
X.set_at((j, i), l[i][j])
return X
def get_list(r):
_ = r.recvline()
Y = []
for i in range(6):
item = r.recvline()
Y.append([i for i in map(int,item.strip().replace(b'[',b'').replace(b']',b'').split(b','))])
return Y
def decrypt(r, bytes_Y, n, p):
r.sendline('2')
_ = r.recvuntil('Data: ')
r.sendline(b64encode(bytes_Y))
X = get_list(r)
X = list2FGLG(n, p, X)
return X
n = 6
r = remote('127.0.0.1', 23456)
Y = get_list(r)
_ = r.recvuntil('p = ')
p = int(r.recvline().strip())
Y = list2FGLG(n, p, Y)
_ = r.recv()
Xlist = [[0]*6 for _ in range(6)]
count = 0
for i in range(n):
for j in range(n):
ct = b'\x00' * count + b'\x01' + b'\x00' * (n*n-count-1)
Xlist[i][j] = decrypt(r, ct, n, p)
count += 1
X = FiniteGeneralLinearGroup(n, p)
for i in range(n):
for j in range(n):
X += Xlist[i][j] * Y.get_at((j, i))
flag = ''
for i in range(n):
for j in range(n):
flag += chr(X.get_at((j, i)))
print(flag)
执行exp即可恢复出flag:
zer0pts{r1ng_h0m0m0rph1sm_1s_c00l}
参考
https://en.wikipedia.org/wiki/Paillier_cryptosystem
https://en.wikipedia.org/wiki/Shamir%27s_Secret_Sharing
https://crypto.stackexchange.com/questions/11053/rsa-least-significant-bit-oracle-attack


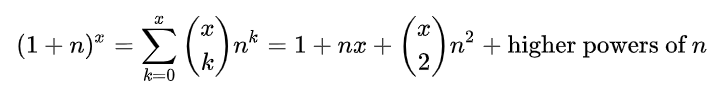
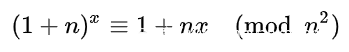







发表评论
您还未登录,请先登录。
登录