硬件安全系列 第一篇 逻辑电路基础知识介绍（一）

 

前言

我带着新的系列又来了，之前的自动化代码审计工具还会在之后分享实际编写的过程思路以及代码。
新的系列是硬件安全，非常庞大的知识体系，我只是分享部分我所学习到的。会包括VLSI Testing ,Hareware Implementation of hash functions ,RSA Implementation and Security,Security Based on Physical Unclonability and Discoder,Hardware Metering,Digital Watermark,Physical attacks and tamper resistance,side channel attacks ,trusted design in FPGAs,security in embedded systems ,security for RFID Tags,Memory integrity protection,hardware trojans.这个框架是由Introduction to Hardware Security and Trust提供的。其中的知识内容会包括coursera中的大量课程以及大量书籍中内容。这一篇的内容包括Hardware Security by GangQu and VLSI CAD Part I: Logic 以及书中内容

首先是逻辑电路部分的基础知识。

 

Digital System

数字系统

一个系统可以看作一个黑盒，这个黑盒处理输入生成输出，输入和输出之间的关系定义为功能。

作为处理现实生活应用的一个数字系统，首先要处理的就是现实和数字之间的关系。现实生活中的信号是连续的，但是数字信号不能完美的复现，所以我们只能将连续的信号分割，用机械化的数字信号近似表示，如同微分。

basic logic gates

基本逻辑门

and xy

or x+y

not ^x

常用的由上述三个基本逻辑门构成的复杂逻辑门

NAND ^(xy)

NOR ^(x+y)

XOR (^xy+x^y)

XNOR ^(^xy+x^y)

design

将一个实际问题转换成电路图我们要明确实际问题的输入输出关系列表表示，得到最简逻辑表达式，选择触发器，明确特定输入，简化电路图。

第一步明确实际问题输入输出：将所有数据转换成二进制

第二步列表

第三步得到最简逻辑关系和对应的电路图

combinational and sequential

组合与时序逻辑

组合逻辑就是无论在什么时候什么环境相同输入对应相同输出

时序逻辑就是相同输入会对应不同输出，而相同输入不同输出的原因就是时序逻辑中包含了存储功能，可以存储状态。而这不同的状态就导致相同输入会出现不同输出。

combinational例子

设计一个数字电路，判断输入月份是否有31天。

首先月份有12个月，1，2，3 … 12。分别用二进制表示就是4位二进制数。从0001到1100。有31天我们用1表示，没有用0表示。

接着用表格表示这些数据之间的关系

我们寻找ABCD与F的逻辑关系

从现实角度：1 3 5 7 8 10 12我们可以看到7为分界线，7之前都是奇数，8之后都是偶数。8在二进制中是1000，奇数D为1，偶数D为0，7之前A为0，7之后A为1，我们可以猜测ABCDF逻辑关系F=A XOR D

从真值表角度：前7行我们发现D和F一致，7之后D和F为反。7之前和之后的区别在于A从0到1。所以得到F = A XOR D

最后构造电路图

the different between sequential and combinational in harfware basic memory unit

时序逻辑能够对相同输入产生不同输出的原因就是其中有基本的存储单元实现状态存储

Flip-flop

触发器

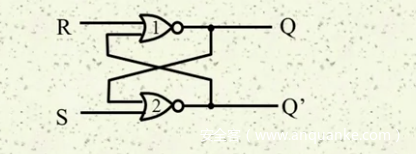
这个触发器可以看到是两个输出两个输出，逻辑门是两个或非门。接下来我们做出真值表

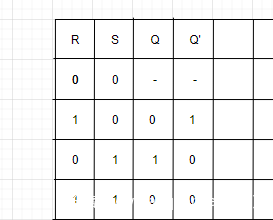
我们可以看到RS输入是00时，Q和Q‘不能得到答案，

在Q Q’原本是00状态下输入00输出无法稳定

原状态10输入00为01

原状态01输入00为10

也就是当我们输入00时，输出会变成原来输出的非运算结果。

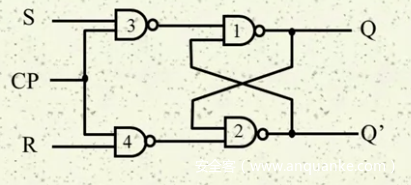
这个逻辑关系中右半部分可以看到和我们之前分析的二输入二输出的逻辑电路图很像。我们先对右边进行分析，列出真值表。

同样的只有输入11是不确定的，在原状态为11时，输出为无法稳定，原状态10 输出为10 原状态01 输出为01

接下来我们来看看左边部分电路图对逻辑的影响：

当CP为0时，无论RS输入是什么，右边逻辑输入都会是00，其余状态下不影响。也就是我们存在一个接口可以让我们一键控制。

Boolean Decompositions

Shannon Expansion

对于一个函数F(x_1 ,x_2,….x_n)，为了得到对于特定x_i的展开式，F可以改写成 x_i F(x_i=1) + ^x_i F(x_i=0)。当对更多x_i展开时，可以改写成x_i y_i F(x_i=1,y_i=1) + x_i ^y_i F(x_i=1,y_i=0) + ^x_i y_i F(x_i=0,y_i=1)+ ^x_i ^y_i F(x_i=0,y_i=0) = F(x,y,w,z)从而简化表达式

Boolean Difference

əf / əx = f(x_i) ⊕ f(^x_i) (异或 xor 不同就是1 相同就是0)

əf / əxəy = əf / əyəx

ə(f ⊕ g) / əx = əf / əx ⊕ əg / əx

设定x为1 判断 f(x) 和 f(^x)

for gate-level: not əf / əx = 1 and əf / əx = y (y为1,x变则变)

or əf / əx = ^y （y为0,x变则变） xor əf / əx = 1

首先，异或的逻辑，相同为0，不同为1。有没有想到什么数学知识。导数，当x改变时，y不变，则导数为0，否则不等于0。在硬件当中，执行异或操作的两个输入相同则为0，不同则为1。

所以我们引入əf / əx = f(x_i) ⊕ f(^x_i) 实现判断x_i是否影响F

从逻辑门的角度理解，我们得到not这个F一定受x影响（由于not单输入，输入改变输出一定改变），and这个F当y为1时受影响，0不受影响（and逻辑门有0出0全1出1），or这个F当y为0时受影响，1时不受影响（or逻辑门有1出1，全0出0），xor也受x_i影响（由于xor逻辑门同为0，异为1，当改变一个输入，两个输入之间的关系一定改变）

Quantification Operators

首先，介绍定义quantification（量化）。量化就是对一个逻辑输入赋值，可以是全部，也可以是任意一个。

universal quantification

全部量化

全部量化就是赋值逻辑输入为全部，也就是对任何x所属范围的真实值都满足量化后条件。

我们举个现实例子

2 0 = 0 + 0 2 1 = 1 + 1 ……

我们可以归纳成2 * n = n + n对于任意实数满足条件

在数字电路中，我们可以用下面的形式表示全部量化

(∨x_i F)[x_1,x_2 … x_n]

(∨xy F)[x_1,x_2 … x_n] = (∨x(∨y F)) =Fxy Fx’y Fxy’ Fx’y’

对于所有 x y 都满足F 为1，也就是x y不影响F

existential quantification

存在量化

相对应的，存在量化就是我们归纳的结果在特定条件下能够满足原逻辑。

数字电路中的表示如下

(ヨx_i F)[x_1,x_2 … x_n]

(ヨxy F)[x_1,x_2 … x_n] = (ヨx(ヨy F)) =Fxy + Fx’y + Fxy’ + Fx’y’

存在x y 满足 F 不受 xy 影响

Network Repair

当一个逻辑门出现问题时，添加一个4输入的逻辑电路和原输入进行操作，使得最终结果符合原逻辑。选择4输入的原因是我们可以凭借这四个输入构造所有的逻辑关系。

F是正常操作下的结果，G是当前操作的结果

我们需要做到的是无论F的输入是什么，我们的G要和F一致

即满足z = ! (F xor G)

在这个新的关系中，有原输入a b ，新的输入d_0,d_1,d_2,d_3，以及输出z。我们要实现无论a b是什么，要找到d_0,d_1,d_2,d_3满足最终结果恒为1

即(∨ab,z)[d_0,d_1,d_2,d_3] == 1

Recursive Tautology

递归重复

对于上面的修复方法，我们需要知道的是是否所有a b都满足结果为1。而验证方法就是递归重复。

如果说仅仅是盲目的递归重复，毫无疑问，这会是一个极其巨大的工程量。所以我们要用科学的递归重复实现目标。

首先，我们要表示逻辑，我们引入PCN

PCN Positional Cube Notation

PCN 是什么，一种符号表示。对于任何输入，用10/01/11表示，其中01表示x，10表示x’，11表示无影响。

比如：f(a,b,c) = a + bc + ab => {01 11 11},{11,01,01},{01,01,11}

接下来就是如何科学递归。

对于一个F总是结果为1，首先要满足对于其中任意一个输入都有F(x=0) = 1以及 F(x=1) = 1。也就是我们可以减少输入的存在从而减少递归的工程量。

那么，我们选取哪些输入以及减少到什么程度时判断呢。

首先是输入的选择

对于F(x=1)，我们将包含x’的部分忽略，忽略x的存在，保留其他。因为x=1时，x’=0，在一个单独的因子中，显然这个因子会返回0，而在所有因子的集合中，由于是0，所以不用考虑。而x=1在因子中也不占决定地位（and 全一出一有零出零）

对于F(x=0)，我们将包含x的部分忽略，忽略x’的存在，保留其他。因为x=0时，x=0，在一个单独的因子中，显然这个因子会返回0，而在所有因子的集合中，由于是0，所以不用考虑。而x‘=1在因子中也不占决定地位（and 全一出一有零出零）

然后是判断开始条件

当存在一个因子恒为1时，成立。当x和x’都单独作为因子恒为1。

除此之外存在一种状况我们可以明确得出f不恒为1：f中所有因子包含的元素不存在x 和 x’的关系，即改变x一定会对f造成一定影响。当所有元素取反时，f一定变化。我们将f中所有因子包含的元素不存在x 和 x’的关系定义为unate

由于unate形式的特殊性，当我们无法立马辨别当前f是否满足条件时，我们尽量将提取一个元素使得f变成unate形式。同时我们利用F = xF(X=1) + ^x\F(x=0)使得结果具有一致性。

伪代码

tautology(f represented as cubelist){  //01 10 11
    if (f is unate){
        apply unate rules
        if(==1) return 1
        else return 0
    }
    else if(x and x'){
        return 1
    }
    else {
        x = most not unate variable in f
        return(tautology(f_x)&&tautology(f_x'))
    }
}