MathJax.Hub.Config({tex2jax: {inlineMath: [[‘$’,’$’], [‘\(‘,’\)’]]}});
大家好,我是FlappyPig的队长bibi,近期因为一些比赛以及其他原因,总结了一些RSA方面的东西,于是在这里与大家分享,希望大家能有所收获,如有不当之处敬请批评指正。
0x01 前言
这里就不讨论数论的基础了,进行RSA的题目解答,至少要懂得基本的数论知识的,如果不了解数论的基本知识的话,网上相关内容还是挺多的。
RSA基于一个简单的数论事实,两个大素数相乘十分容易,将其进行因式分解确实困难的。在量子计算机还没有成熟的今天,RSA算法凭借其良好的抵抗各种攻击的能力,在公钥密码体制中发挥着中流砥柱的作用。然而即便RSA算法目前来说是安全可靠的,但是错误的应用场景,错误的环境配置,以及错误的使用方法,都会导致RSA的算法体系出现问题,从而也派生出针对各种特定场景下的RSA攻击方法。
本文针对一些在CTF中常见的RSA攻击方法,从如何识别应该应用那种方法以及如何去解题来介绍CTF中的RSA题目的常见解法。
RSA算法描述
RSA算法涉及三个参数,n,e,d,私钥为n,d,公钥为n,e。
其中n是两个大素数p,q的乘积。
d是e模$ varphi(n) $的逆元,$ varphi(n) $是n的欧拉函数。
c为密文,m为明文,则加密过程如下:
$ cequiv m^e mod n $
解密过程如下:
$ mequiv c^d$ $mod$ $n$
n,e是公开的情况下,想要知道d的值,必须要将n分解计算出n的欧拉函数值,而n是两个大素数p,q的乘积,将其分解是困难的。
RSA题目类型
在CTF竞赛中,RSA理所当然处在CRYPTO中居多。而且RSA作为典型的加密算法,其出镜率可谓相当高,基本上所有比赛都会有几道RSA的题目出现。
数据处理
在进行做题之前,我们要将数据处理成可以做题的模式。基本上来说,RSA的题目都是围绕着c,m,e,d,n,p,q这几个参数展开的,但是题目一般不会直接给这种样子的参数,而是通过别的方式给出,这里就需要我们使用一些工具或者自己手工将这些参数提取出来。
pem文件:针对此类文件可以直接使用openssl提取,大概使用过的方式有:
openssl rsautl -encrypt -in FLAG -inkey public.pem -pubin -out flag.enc
openssl rsa -pubin -text -modulus -in warmup -in public.pempcap文件:针对此类文件可以使用wireshark follow一下。这种问题一般都是写了一个交互的crypto系统,所以可能产生多轮交互。
PPC模式:这种模式是上述pcap文件的交互版,会给一个端口进行一些crypto的交互,参数会在交互中给出。
第二个需要处理的就是明密文,这个方法多多,不多赘述。
0x02 模数分解
说一说
解决RSA题目最简单,最暴力,最好使的方法就是分解模数n。如果能够将n分解成功,成功得到p,q的取值,那么可求n的欧拉函数的值。
$ varphi(n)=(p-1)(q-1) $
而通过e,d与n的欧拉函数满足如下关系:
$ed=1$ $mod$ $varphi(n) $
通过欧几里得算法可以通过e与n的欧拉函数的值轻易求出d,从而计算出解密密钥。
即在知道e,p,q的情况下,可以解出d:
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('modular inverse does not exist')
else:
return x % mmodinv函数即为求模拟的函数,在知道e,p,q的情况下,可以:
d=modinv(e,(p-1)*(q-1))即可求出解密密钥。
写到这里,要提出一个细节问题,在利用python进行rsa的题目求解过程中:
$ cequiv m^e mod n $
此类运算需要使用pow函数来进行求解,而不是直接m**e % n,这样会慢死的。Python在处理此类运算进行了优化。比如刚才在已知p,q的时候利用modinv函数求出了d,然后就可以利用pow函数求出明文:
m=pow(c,d,n)例题:
https://www.jarvisoj.com (very easy RSA)
题目中直接给了p,q,e。
可以直接求出d:
p = 3487583947589437589237958723892346254777
q = 8767867843568934765983476584376578389
e = 65537
d = modinv(e, (p-1)*(q-1))
print d
直接分解n
介绍:
素数分解问题是困难的,但是可以通过计算机进行暴力分解。1999年,名为Cray的超级计算机用了5个月时间分解了512bit的n。2009年,一群研究人员成功分解了768bit的n。2010年,又提出了一些针对1024bit的n的分解的途径,但是没有正面分解成功。通常意义上来说,一般认为2048bit以上的n是安全的。现在一般的公钥证书都是4096bit的证书。
如果n比较小,那么可以通过工具进行直接n分解,从而得到私钥。如果n的大小小于256bit,那么我们通过本地工具即可爆破成功。例如采用windows平台的RSATool2v17,可以在几分钟内完成256bit的n的分解。
如果n在768bit或者更高,可以尝试使用一些在线的n分解网站,这些网站会存储一些已经分解成功的n,比如:http://factordb.com
通过在此类网站上查询n,如果可以分解或者之前分解成功过,那么可以直接得到p和q。然后利用前述方法求解得到密文。
识别:
此类问题一般是分值较小的题目,提取出n之后可以发现n的长度小于等于512bit,可以直接取分解n。如果大于512bit,建议在使用每个题目都用后面所说的方法去解题。
例题:
比如在某次竞赛中,发现:
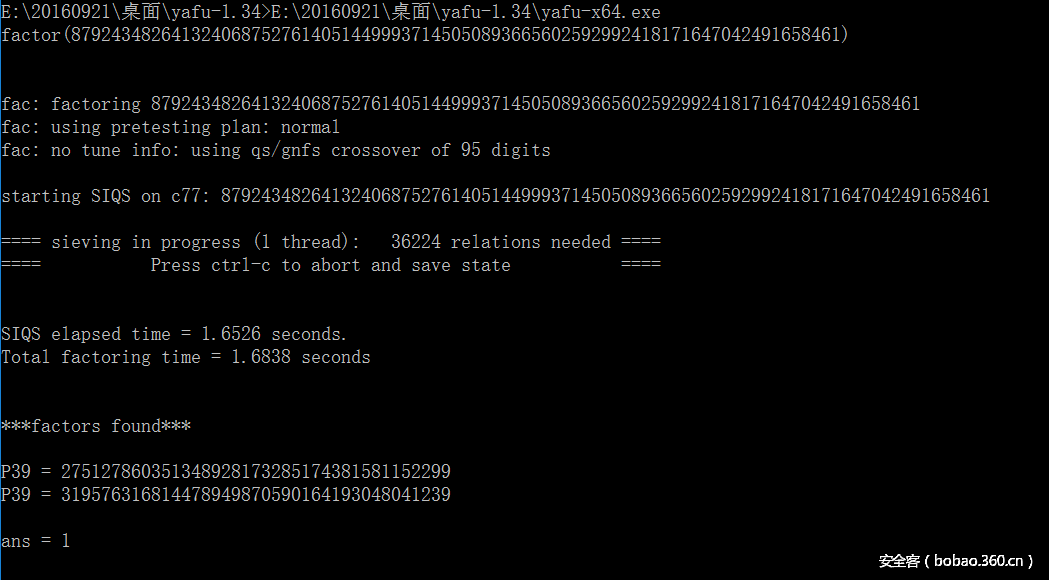
n=87924348264132406875276140514499937145050893665602592992418171647042491658461
利用factordb分解:
利用公约数
介绍:
如果在两次公钥的加密过程中使用的$n_1$ 和$n_2$具有相同的素因子,那么可以利用欧几里得算法直接将$n_1$和$n_2$分解。
通过欧几里得算法可以直接求出$n_1$和$n_2$的最大公约数p:
$(n1,n2)=p$
可以得出:
$n_1=p$$q_1$
$n_2=p$$q_2$
直接分解成功。而欧几里得算法的时间复杂度为:O(log n)。这个时间复杂度即便是4096 bit也是秒破级别。
def gcd(a, b):
if a < b:
a, b = b, a
while b != 0:
temp = a % b
a = b
b = temp
return a识别此类题目,通常会发现题目给了若干个n,均不相同,并且都是2048bit,4096bit级别,无法正面硬杠,并且明文都没什么联系,e也一般取65537。 识别:
例题:
在一个题目中,你拿到了两个n,e都为65537,两个n分别为:
n1=9051013965404084482870087864821455535159008696042953021965631089095795348830954383127323853272528967729311045179605407693592665683311660581204886571146327720288455874927281128121117323579691204792399913106627543274457036172455814805715668293705603675386878220947722186914112990452722174363713630297685159669328951520891938403452797650685849523658191947411429068829734053745180460758604283051344339641429819373112365211739216160420494167071996438506850526168389386850499796102003625404245645796271690310748804327
n2=13225948396179603816062046418717214792668512413625091569997524364243995991961018894150059207824093837420451375240550310050209398964506318518991620142575926623780411532257230701985821629425722030608722035570690474171259238153947095310303522831971664666067542649034461621725656234869005501293423975184701929729170077280251436216167293058560030089006140224375425679571181787206982712477261432579537981278055755344573767076951793312062480275004564657590263719816033564139497109942073701755011873153205366238585665743通过直接分解,上factordb都分解失败。通过尝试发现:
print gcd(n1,n2)打印出:
1564859779720039565508870182569324208117555667917997801104862601098933699462849007879184203051278194180664616470669559575370868384820368930104560074538872199213236203822337186927275879139590248731148622362880471439310489228147093224418374555428793546002109
则此致即为两个n共有的素因子p,然后进一步求出q,求解完毕。
Fermat方法与Pollard rho方法
介绍:
针对大整数的分解有很多种算法,性能上各有优异,有Fermat方法,Pollard rho方法,试除法,以及椭圆曲线法,连分数法,二次筛选法,数域分析法等等。其中一些方法应用在RSA的攻击上也有奇效。
在p,q的取值差异过大,或者p,q的取值过于相近的时候,Format方法与Pollard rho方法都可以很快将n分解成功。
此类分解方法有一个开源项目yafu将其自动化实现了,不论n的大小,只要p和q存在相差过大或者过近时,都可以通过yafu很快地分解成功。
识别:
在直接分解n无望,不能利用公约数分解n之后,都应该使用yafu去试一下。
例题:
https://www.jarvisoj.com (Medium RSA)
此题首先从pem中提取N和e,然后上yafu,直接分解成功。
0x03 低加密指数攻击
在RSA中e也称为加密指数。由于e是可以随意选取的,选取小一点的e可以缩短加密时间,但是选取不当的话,就会造成安全问题。
e=3时的小明文攻击
介绍:
当e=3时,如果明文过小,导致明文的三次方仍然小于n,那么通过直接对密文三次开方,即可得到明文。
即:
$ cequiv m^e$ $mod$ $n$
如果e=3,且$ m^e<{n} $,那么:
$ c= m^e,$ $e=3$
$ m=sqrt[3]{c}$
如果明文的三次方比n大,但是不是足够大,那么设k,有:
$ c= m^e+kn$
爆破k,如果$ c-kn $能开三次根式,那么可以直接得到明文。
识别:
推荐在e=3的时候首先尝试这种方法。
例题:
https://www.jarvisoj.com (Extremely hard RSA)
关键代码如下:此题通过不断给明文+n开三次方即可求得:
i=0
while 1:
if(gmpy.root(c+i*N, 3)[1]==1):
print gmpy.root(c+i*N, 3)
break
i=i+1
低加密指数广播攻击
介绍:
如果选取的加密指数较低,并且使用了相同的加密指数给一个接受者的群发送相同的信息,那么可以进行广播攻击得到明文。
即,选取了相同的加密指数e(这里取e=3),对相同的明文m进行了加密并进行了消息的传递,那么有:
$ c_1equiv m^e$ $mod$ $n_1$
$ c_2equiv m^e$ $mod$ $n_2$
$ c_3equiv m^e$ $mod$ $n_3$
对上述等式运用中国剩余定理,在e=3时,可以得到:
$ c_xequiv m^3$ $mod$ $n_1n_2n_3$
通过对$ c_x $进行三次开方可以求得明文。
识别:
这个识别起来比较简单,一般来说都是给了三组加密的参数和明密文,其中题目很明确地能告诉你这三组的明文都是一样的,并且e都取了一个较小的数字。
例题:
SCTF2016,CODE300
题目第二轮中通过流量包的方式给了广播攻击的参数。
这里我就不卖萌了,直接给国外类似一题的网址:http://codezen.fr/2014/01/16/hackyou-2014-crypto-400-cryptonet
Coppersmith定理攻击
Coppersmith定理指出在一个e阶的mod n多项式f(x)中,如果有一个根小于$ n^frac{1}{e} $,就可以运用一个O(log n)的算法求出这些根。
这个定理可以应用于RSA算法。如果e = 3并且在明文当中只有三分之二的比特是已知的,这种算法可以求出明文中所有的比特。
并未找到真题。
0x04 低解密指数攻击
介绍:
与低加密指数相同,低解密指数可以加快解密的过程,但是者也带来了安全问题。Wiener表示如果满足:
$ d<frac{1}{3}gn^frac{1}{4}$
那么一种基于连分数(一个数论当中的问题)的特殊攻击类型就可以危害RSA的安全。此时需要满足:
$q<$$p$$<2q$
如果满足上述条件,通过Wiener Attack可以在多项式时间中分解n。
rsa-wiener-attack的攻击源码开源在了github中,采取python编写,可以很容易使用。
识别:
非常简单,e看起来很大就行了。
例题:
直接github用工具就行。https://github.com/pablocelayes/rsa-wiener-attack
这里注意一个细节问题,如果在运行脚本的时候报错,请在脚本前加上:
import sys
sys.setrecursionlimit(10000000)
0x05 共模攻击
介绍:
如果在RSA的使用中使用了相同的模n对相同的明文m进行了加密,那么就可以在不分解n的情况下还原出明文m的值。
即:
$ c_1equiv m^{e_1}$ $mod$ $n$
$ c_2equiv m^{e_2}$ $mod$ $n$
此时不需要分解n,不需要求解私钥,如果两个加密指数互素,就可以通过共模攻击在两个密文和公钥被嗅探到的情况下还原出明文m的值。
过程如下,首先两个加密指数互质,则:
$ (e_1,e_2)=1 $
即存在$ s_2 $,$ s_2 $使得:
$ s_1e_1+s_2e_2=1 $
又因为:
$ c_1equiv m^{e_1}$ $mod$ $n$
$ c_2equiv m^{e_2}$ $mod$ $n$
通过代入化简可以得出:
$c_1^{s_1}c_2^{s_2}equiv m$ $mod$ $n$
明文解出。
识别:
非常简单,若干次加密,每次n都一样,明文根据题意也一样即可。
例题:
https://www.jarvisoj.com (very hard RSA)
如果已知:n1,n2,c1,c2,e1,e2,并且其中n1=n2的话:
s = egcd(e1, e2)
s1 = s[1]
s2 = s[2]
print s
n=n1
if s1<0:
s1 = - s1
c1 = modinv(c1, n)
elif s2<0:
s2 = - s2
c2 = modinv(c2, n)
m=(pow(c1,s1,n)*pow(c2,s2,n)) % n
0x06 总结
这里总结方法也不是全部的方法,但是希望能够对大家RSA方面解题过程中能提供一些帮助。这里推荐汪神的OJ系统,里面题目多多,关于RSA也有不少,可以在此练习:https://www.jarvisoj.com
顺便再打个广告,我们战队最近正在从战队角度编篡一本CTF方面相关的书籍,干货多多,敬请期待!
本文如有什么问题或建议,请联系我,一定虚心接受:bibi@flappypig.club。










发表评论
您还未登录,请先登录。
登录