前言
在watevrCTF 2019中有4道Crypto方向的题目,题目难度适中,在这里对题目进行一下分析。
Swedish RSA
题目描述如下:
Also known as Polynomial RSA. This is just some abstract algebra for fun!
Files:polynomial_rsa.sage, polynomial_rsa.txt
分析一下源码,发现题目实现了一个基于多项式的RSA算法,对于考察这种形式的题目,一般模数N都可以直接分解成两个多项式的乘积,所以题目难度通常不大,唯一需要注意一下的是对于基于多项式的RSA算法,其phi的表达式是不同的,根据这篇论文,我们可以得知phi值的表达式(即文中的s)为:
这里的p需要注意一下,它指的是我们的多项式的系数有多少种可能的值,关于这个我们可以回到欧拉函数的定义去理解:
对于整数n来讲,欧拉函数phi(n)表示所有小于或等于n的正整数中与n互质的数的数目。
对于多项式P(y)来讲,欧拉函数phi(P(y))表示所有不高于P(y)幂级的环内所有多项式中,与P(y)无除1以外的公因式的其他多项式的个数。
我们本题当中的P(x)和Q(x)是多项式GF(p)上的,因此这里phi的值应该等于(p**P(x).degree()-1)*(p**Q(x).degree()-1)。有兴趣的读者可以回忆一下今年0CTF/TCTF 2019 Quals当中的Baby RSA那道题,当时那道题目的P(x)和Q(x)是GF(2)上的,因此phi等于(2**P(x).degree()-1)*(2**Q(x).degree()-1),读者可以比较一下两道题目来体会其中的异同。
知道phi值之后,其余按照正常步骤计算即可,可以写出脚本如下:
from binascii import *
P = 43753
R.<y> = PolynomialRing(GF(P))
N = 34036*y^177 + 23068*y^176 + 13147*y^175 + 36344*y^174 + 10045*y^173 + 41049*y^172 + 17786*y^171 + 16601*y^170 + 7929*y^169 + 37570*y^168 + 990*y^167 + 9622*y^166 + 39273*y^165 + 35284*y^164 + 15632*y^163 + 18850*y^162 + 8800*y^161 + 33148*y^160 + 12147*y^159 + 40487*y^158 + 6407*y^157 + 34111*y^156 + 8446*y^155 + 21908*y^154 + 16812*y^153 + 40624*y^152 + 43506*y^151 + 39116*y^150 + 33011*y^149 + 23914*y^148 + 2210*y^147 + 23196*y^146 + 43359*y^145 + 34455*y^144 + 17684*y^143 + 25262*y^142 + 982*y^141 + 24015*y^140 + 27968*y^139 + 37463*y^138 + 10667*y^137 + 39519*y^136 + 31176*y^135 + 27520*y^134 + 32118*y^133 + 8333*y^132 + 38945*y^131 + 34713*y^130 + 1107*y^129 + 43604*y^128 + 4433*y^127 + 18110*y^126 + 17658*y^125 + 32354*y^124 + 3219*y^123 + 40238*y^122 + 10439*y^121 + 3669*y^120 + 8713*y^119 + 21027*y^118 + 29480*y^117 + 5477*y^116 + 24332*y^115 + 43480*y^114 + 33406*y^113 + 43121*y^112 + 1114*y^111 + 17198*y^110 + 22829*y^109 + 24424*y^108 + 16523*y^107 + 20424*y^106 + 36206*y^105 + 41849*y^104 + 3584*y^103 + 26500*y^102 + 31897*y^101 + 34640*y^100 + 27449*y^99 + 30962*y^98 + 41434*y^97 + 22125*y^96 + 24314*y^95 + 3944*y^94 + 18400*y^93 + 38476*y^92 + 28904*y^91 + 27936*y^90 + 41867*y^89 + 25573*y^88 + 25659*y^87 + 33443*y^86 + 18435*y^85 + 5934*y^84 + 38030*y^83 + 17563*y^82 + 24086*y^81 + 36782*y^80 + 20922*y^79 + 38933*y^78 + 23448*y^77 + 10599*y^76 + 7156*y^75 + 29044*y^74 + 23605*y^73 + 7657*y^72 + 28200*y^71 + 2431*y^70 + 3860*y^69 + 23259*y^68 + 14590*y^67 + 33631*y^66 + 15673*y^65 + 36049*y^64 + 29728*y^63 + 22413*y^62 + 18602*y^61 + 18557*y^60 + 23505*y^59 + 17642*y^58 + 12595*y^57 + 17255*y^56 + 15316*y^55 + 8948*y^54 + 38*y^53 + 40329*y^52 + 9823*y^51 + 5798*y^50 + 6379*y^49 + 8662*y^48 + 34640*y^47 + 38321*y^46 + 18760*y^45 + 13135*y^44 + 15926*y^43 + 34952*y^42 + 28940*y^41 + 13558*y^40 + 42579*y^39 + 38015*y^38 + 33788*y^37 + 12381*y^36 + 195*y^35 + 13709*y^34 + 31500*y^33 + 32994*y^32 + 30486*y^31 + 40414*y^30 + 2578*y^29 + 30525*y^28 + 43067*y^27 + 6195*y^26 + 36288*y^25 + 23236*y^24 + 21493*y^23 + 15808*y^22 + 34500*y^21 + 6390*y^20 + 42994*y^19 + 42151*y^18 + 19248*y^17 + 19291*y^16 + 8124*y^15 + 40161*y^14 + 24726*y^13 + 31874*y^12 + 30272*y^11 + 30761*y^10 + 2296*y^9 + 11017*y^8 + 16559*y^7 + 28949*y^6 + 40499*y^5 + 22377*y^4 + 33628*y^3 + 30598*y^2 + 4386*y + 23814
S.<x> = R.quotient(N)
C = 5209*x^176 + 10881*x^175 + 31096*x^174 + 23354*x^173 + 28337*x^172 + 15982*x^171 + 13515*x^170 + 21641*x^169 + 10254*x^168 + 34588*x^167 + 27434*x^166 + 29552*x^165 + 7105*x^164 + 22604*x^163 + 41253*x^162 + 42675*x^161 + 21153*x^160 + 32838*x^159 + 34391*x^158 + 832*x^157 + 720*x^156 + 22883*x^155 + 19236*x^154 + 33772*x^153 + 5020*x^152 + 17943*x^151 + 26967*x^150 + 30847*x^149 + 10306*x^148 + 33966*x^147 + 43255*x^146 + 20342*x^145 + 4474*x^144 + 3490*x^143 + 38033*x^142 + 11224*x^141 + 30565*x^140 + 31967*x^139 + 32382*x^138 + 9759*x^137 + 1030*x^136 + 32122*x^135 + 42614*x^134 + 14280*x^133 + 16533*x^132 + 32676*x^131 + 43070*x^130 + 36009*x^129 + 28497*x^128 + 2940*x^127 + 9747*x^126 + 22758*x^125 + 16615*x^124 + 14086*x^123 + 13038*x^122 + 39603*x^121 + 36260*x^120 + 32502*x^119 + 17619*x^118 + 17700*x^117 + 15083*x^116 + 11311*x^115 + 36496*x^114 + 1300*x^113 + 13601*x^112 + 43425*x^111 + 10376*x^110 + 11551*x^109 + 13684*x^108 + 14955*x^107 + 6661*x^106 + 12674*x^105 + 21534*x^104 + 32132*x^103 + 34135*x^102 + 43684*x^101 + 837*x^100 + 29311*x^99 + 4849*x^98 + 26632*x^97 + 26662*x^96 + 10159*x^95 + 32657*x^94 + 12149*x^93 + 17858*x^92 + 35805*x^91 + 19391*x^90 + 30884*x^89 + 42039*x^88 + 17292*x^87 + 4694*x^86 + 1497*x^85 + 1744*x^84 + 31071*x^83 + 26246*x^82 + 24402*x^81 + 22068*x^80 + 39263*x^79 + 23703*x^78 + 21484*x^77 + 12241*x^76 + 28821*x^75 + 32886*x^74 + 43075*x^73 + 35741*x^72 + 19936*x^71 + 37219*x^70 + 33411*x^69 + 8301*x^68 + 12949*x^67 + 28611*x^66 + 42654*x^65 + 6910*x^64 + 18523*x^63 + 31144*x^62 + 21398*x^61 + 36298*x^60 + 27158*x^59 + 918*x^58 + 38601*x^57 + 4269*x^56 + 5699*x^55 + 36444*x^54 + 34791*x^53 + 37978*x^52 + 32481*x^51 + 8039*x^50 + 11012*x^49 + 11454*x^48 + 30450*x^47 + 1381*x^46 + 32403*x^45 + 8202*x^44 + 8404*x^43 + 37648*x^42 + 43696*x^41 + 34237*x^40 + 36490*x^39 + 41423*x^38 + 35792*x^37 + 36950*x^36 + 31086*x^35 + 38970*x^34 + 12439*x^33 + 7963*x^32 + 16150*x^31 + 11382*x^30 + 3038*x^29 + 20157*x^28 + 23531*x^27 + 32866*x^26 + 5428*x^25 + 21132*x^24 + 13443*x^23 + 28909*x^22 + 42716*x^21 + 6567*x^20 + 24744*x^19 + 8727*x^18 + 14895*x^17 + 28172*x^16 + 30903*x^15 + 26608*x^14 + 27314*x^13 + 42224*x^12 + 42551*x^11 + 37726*x^10 + 11203*x^9 + 36816*x^8 + 5537*x^7 + 20301*x^6 + 17591*x^5 + 41279*x^4 + 7999*x^3 + 33753*x^2 + 34551*x + 9659
p,q = N.factor()
p,q = p[0],q[0]
s = (P**p.degree()-1)*(P**q.degree()-1)
e = 65537
d = inverse_mod(e,s)
M = C^d
print ("".join([chr(c) for c in M.list()]))
执行脚本即可得到flag:
watevr{RSA_from_ikea_is_fun_but_insecure#k20944uehdjfnjd335uro}
ECC-RSA
题目描述如下:
ECC + RSA = Double security!
Files:ecc-rsa.py, ecc-rsa.txt
分析一下源码,发现题目使用了ECC和RSA两种加密算法,其中flag是通过RSA加密的,我们知道e和n,但无法直接分解n。同时,我们还知道ECC的曲线(y^2 = x^3 + a*x + b)和曲线参数(a、b、P)以及基点G的值,且(p,q)是椭圆曲线上的一点,即:
q^2 ≡ p^3 + a*p + b (mod P)
同余式两边同时乘上p^2,有:
n^2 ≡ p^5 + a*p^3 + b*p^2 (mod P)
设f ≡ p^5 + a*p^3 + b*p^2 - n^2(mod P),此时多项式f中只有p这一个未知数。我们可以尝试对f分解,在其因式中找到其中度为1的多项式(即p+C这种形式,其中C为任意整数),然后判断该多项式的解和n是否存在1以外的公因子,若存在,则可以认为解出p(需要注意,如果计算出来的解为负数,需要将其对P取模来模正),此时计算n/p即可得到q,从而实现模数n的分解。
将上述推导写成代码形式如下:
from binascii import *
P = 0x1ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
a = -0x3
b = 0x51953eb9618e1c9a1f929a21a0b68540eea2da725b99b315f3b8b489918ef109e156193951ec7e937b1652c0bd3bb1bf073573df883d2c34f1ef451fd46b503f00
n = 0x118aaa1add80bdd0a1788b375e6b04426c50bb3f9cae0b173b382e3723fc858ce7932fb499cd92f5f675d4a2b05d2c575fc685f6cf08a490d6c6a8a6741e8be4572adfcba233da791ccc0aee033677b72788d57004a776909f6d699a0164af514728431b5aed704b289719f09d591f5c1f9d2ed36a58448a9d57567bd232702e9b28f
c = 0x3862c872480bdd067c0c68cfee4527a063166620c97cca4c99baff6eb0cf5d42421b8f8d8300df5f8c7663adb5d21b47c8cb4ca5aab892006d7d44a1c5b5f5242d88c6e325064adf9b969c7dfc52a034495fe67b5424e1678ca4332d59225855b7a9cb42db2b1db95a90ab6834395397e305078c5baff78c4b7252d7966365afed9e
R.<X> = PolynomialRing(GF(P))
f = x^5 + a*x^3 + b*x^2 - n^2
factors = f.factor()
for i in factors:
i = i[0]
if i.degree()==1:
tmp = Integer(mod(-i[0],P))
if gcd(tmp,n) != 1:
p = tmp
q = n/tmp
phi = (p-1)*(q-1)
d = inverse_mod(e,phi)
m = pow(c,d,n)
print unhexlify(hex(Integer(m)))
执行脚本即可得到flag:
watevr{factoring_polynomials_over_finite_fields_is_too_ez}
Crypto over the intrawebs
题目描述如下:
I was hosting a very secure python chat server during my lunch break and I saw two of my classmates connect to it over the local network. Unfortunately, they had removed most of the code when i came up to them. I don’t know what they said, can you help me figure it out?
Files:conversation, super_secure_client_1.py, super_secure_client_2.py, super_secure_server.py
审计源码,猜测通信的内容经过了encrypt函数的加密,其加密算法是可逆的,但是我们不知道key,但是观察发现每次加密时,会先在明文前面加上USERNAME + ": "这一前缀,而这一前缀是已知的,因此我们可以使用已知明文攻击的思路,通过解方程组来尝试恢复秘钥。
以Conversion文件中第一条记录为例,根据Message from: 198.51.100.0我们可知其使用的前缀为Houdini:,共计8个字符,根据加密时使用的递推表达式:
out[i+2] == (out[i+1] + ((out[i] * ord(plaintext[i])) ^ (key+out[i+1]))) ^ (key*out[i]) i=0,1,2...
其中out[0]=8886,out[1]=42
可知为了利用上Houdini:这8个字符来列方程需要out数组的前10个值,这里我们采用z3来解方程,先打印出z3格式的方程组:
out = [8886,42,212351850074573251730471044,424970871445403036476084342,5074088654060645719700112791577634658478525829848,17980375751459479892183878405763572663247662296,121243943296116422476619559571200060016769222670118557978266602062366168,242789433733772377162253757058605232140494788666115363337105327522154016,2897090450760618154631253497246288923325478215090551806927512438699802516318766105962219562904,7372806106688864629183362019405317958359908549913588813279832042020854419620109770781392560]
plaintext = "Houdini:"
for i in range(8):
print 's.add('+'(('+str(out[i+1])+'+('+str((out[i] * ord(plaintext[i])))+'^key+'+str(out[i+1])+'))) ^ (key*'+str(out[i])+')'+'=='+str(out[i+2])+')'
然后我们把输出的内容作为约束,但是在设key为BitVec变量时我们发现此时我们还不知道key的bit数,但是鉴于其取值范围比较小(最大为77比特),我们可以依次尝试可能的比特数,然后把解出来的key作为密钥去解密,直到解密出的内容中包含flag:
from z3 import *
def decrypt(ciphertext,key):
out = ciphertext
plaintext = ''
for i in range(2,len(ciphertext)):
p = chr((((out[i] ^ (key*out[i-2])) - out[i-1]) ^ (key+out[i-1]))//out[i-2])
plaintext += p
return plaintext
for i in range(0,77+1)[::-1]:
key = BitVec('key',i)
s = Solver()
s.add(((42+(639792^key+42))) ^ (key*8886)==212351850074573251730471044)
s.add(((212351850074573251730471044+(4662^key+212351850074573251730471044))) ^ (key*42)==424970871445403036476084342)
s.add(((424970871445403036476084342+(24845166458725070452465112148^key+424970871445403036476084342))) ^ (key*212351850074573251730471044)==5074088654060645719700112791577634658478525829848)
s.add(((5074088654060645719700112791577634658478525829848+(42497087144540303647608434200^key+5074088654060645719700112791577634658478525829848))) ^ (key*424970871445403036476084342)==17980375751459479892183878405763572663247662296)
s.add(((17980375751459479892183878405763572663247662296+(532779308676367800568511843115651639140245212134040^key+17980375751459479892183878405763572663247662296))) ^ (key*5074088654060645719700112791577634658478525829848)==121243943296116422476619559571200060016769222670118557978266602062366168)
s.add(((121243943296116422476619559571200060016769222670118557978266602062366168+(1977841332660542788140226624633992992957242852560^key+121243943296116422476619559571200060016769222670118557978266602062366168))) ^ (key*17980375751459479892183878405763572663247662296)==242789433733772377162253757058605232140494788666115363337105327522154016)
s.add(((242789433733772377162253757058605232140494788666115363337105327522154016+(12730614046092224360045053754976006301760768380362448587717993216548447640^key+242789433733772377162253757058605232140494788666115363337105327522154016))) ^ (key*121243943296116422476619559571200060016769222670118557978266602062366168)==2897090450760618154631253497246288923325478215090551806927512438699802516318766105962219562904)
s.add(((2897090450760618154631253497246288923325478215090551806927512438699802516318766105962219562904+(14081787156558797875410717909399103464148697742634691073552108996284932928^key+2897090450760618154631253497246288923325478215090551806927512438699802516318766105962219562904))) ^ (key*242789433733772377162253757058605232140494788666115363337105327522154016)==7372806106688864629183362019405317958359908549913588813279832042020854419620109770781392560)
s.check()
res = s.model()
res = res[key].as_long().real
ans = ''
msg = open('conversation','rb').readlines()
for i in range(1,len(msg),2):
tmp = map(int,msg[i].split('Content: ')[1].split(' '))
ans += decrypt(tmp,res)
if 'watevr{' in ans:
print ans
break
执行脚本即可恢复出通信内容如下:
Houdini: uhm, is this thing working?
nnewram: yeah, hi
Houdini: hi nnew
Houdini: so eh, do you have it?
nnewram: id ont know what you mean
nnewram: *dont
nnewram: have what?
Houdini: :bruh:
Houdini: you know, the thing
nnewram: what, thing?
Houdini: the flag....
nnewram: oooooh
nnewram: right
nnewram: sure let me get it
nnewram: one second
Houdini: kk
nnewram: yeah here you go
nnewram: watevr{Super_Secure_Servers_are_not_always_so_secure}
Houdini: niceeeee
Houdini: thank you
Houdini: oh wait, we should probably remove the code
nnewram: yeah that's actually kinda smart
Houdini: ok cya later
nnewram: cya
在通信内容中发现flag:
watevr{Super_Secure_Servers_are_not_always_so_secure}
Baby RLWE
题目描述如下:
Mateusz carried a huge jar of small papers with public keys written on them, but he tripped and accidentally dropped them into the scanner and made a txt file out of them! D: Note: This challenge is just an introduction to RLWE, the flag is (in standard format) encoded inside the private key.
Files:baby_rlwe.sage, public_keys.txt
RLWE是Ring learning with errors的简称,一个RLWE问题的基本模型如下:
可以看到和我们题目当中给出的符号系统是是一致的,那么我们的任务就是:
b1(x) = a(x)*s(x) + e1(x)
b2(x) = a(x)*s(x) + e2(x)
...
b100(x) = a(x)*s(x) + e100(x)
其中b1(x)到b100(x)已知,a(x)已知,e1(x)到e100(x)未知,求s(x)
通过观察可以发现,这里的a(x)都是通过gen_large_poly()函数生成的,其多项式中x^0、x^1、x^2 … x^(n-1)次方这n项的系数都不为0,其乘上s(x)后,这n项的系数仍然都不为0;而e(x)是通过gen_large_poly()函数生成的,其其多项式中x^0、x^1、x^2 … x^(n-1)次方这n项当中的很多项系数都为0,因此a(x)s(x)再加上e(x)后,得到的结果b(x)当中的很多项的系数是和a(x)s(x)当中对应项的系数是相同的。鉴于我们这里有较多的b(x),因此我们可以进行一个统计,把这100个b(x)当中x^(n-1)这一项的系数中出现频率最高的系数当做是a(x)s(x)当中对应项的系数,把这100个b(x)当中x^(n-2)这一项的系数中出现频率最高的系数当做是a(x)s(x)当中对应项的系数,以此类推,一直到x^0次方,即恢复出a(x)*s(x)的结果,然后将其除以a(x),即得到了s(x)的结果。
从public_keys.txt文件中我们可以发现,b(x)的每一项当中的最高次幂为103,因此n=103+1=104,也即flag的长度为104个字符。另外这里需要注意的是,我们的a(x)和s(x)都是限制在S.<x> = R.quotient(y^n + 1)范围上的,因此我们也要先对每一个b(x)也进行b(x)=S(b(x))的处理,然后再进行运算。我们将上述推导过程写成脚本形式如下:
keys = open("public_keys.txt", "r").read().split("n")[:-1]
keys = open("public_keys.txt", "r").read().split("n")[:-1]
temp1 = keys[0].find("^")
temp2 = keys[0].find(" ", temp1)
n = Integer(keys[0][temp1+1:temp2]) + 1
q = 40961
F = GF(q)
R.<y> = PolynomialRing(F)
S.<x> = R.quotient(y^n + 1)
a = S(keys[0].replace("a: ", ""))
keys = keys[1:]
counters = []
for i in range(n):
counters.append({})
for key in keys:
b = key.replace("b: ", "")
b = list(S(b))
for i in range(n):
try:
counters[i][b[i]] += 1
except:
counters[i][b[i]] = 1
a_s = []
for counter in counters:
dict_keys = counter.keys()
max_key = 0
maxi = 0
for key in dict_keys:
if counter[key] > maxi:
maxi = counter[key]
max_key = key
a_s.append(max_key)
a_s = S(a_s)
s = a_s/a
print ''.join(map(chr,list(s)))
执行脚本即可得到flag:
watevr{rlwe_and_statistics_are_very_trivial_when_you_reuse_same_private_keys#02849jedjdjdj202ie9395u6ky}
参考
http://www.diva-portal.se/smash/get/diva2:823505/FULLTEXT01.pdf
https://en.wikipedia.org/wiki/Ring_learning_with_errors
https://eprint.iacr.org/2012/230.pdf
https://github.com/wat3vr/watevrCTF-2019/tree/master/challenges/crypto


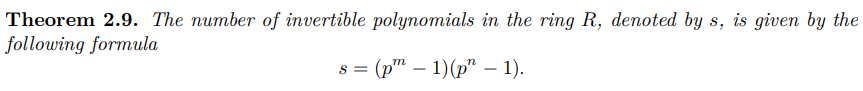








发表评论
您还未登录,请先登录。
登录