前言
本篇是程序分析理论第十一篇:基于类型和响应的系统模型Type and Effect Systems
想法:加入type模型在分析过程中触发响应模型实现函数指向。
基于类型的系统模型 Type System
基于类型的系统模型首先要引入类型要素,类型要素包括bool,类型转换,int。我们分析的语句形式包括:变量,true /false , e e,fn , fun ,let in。
首先,我们做出基于类型的函数语言的语法:
和之前的语法相似,常数为c ,变量为 x,函数fnπ x => e_0 ,递归函数 fun\π f x => e_0 ,并列语句 e_1 e_2 ,if语句 if e_0 then e_1 else e_2 ,函数调用语句 let x = e_1 in e_2 ,判断语句 e_1 op e_2。其中不同的是在函数和递归函数中添加了断点π。
接着,我们提出底层类型模型实现类型判断:
用语句表示就是Γ |- e : t
其中Γ表示 。e表示抽象语句 ,t表示类型
任意 c 存在type,如 true = bool 7 = int
对于任意判断语句参数为int类型,结果为bool类型
应用到所有语句就会变成:
Γ |- c : t_c
Γ |- x : t Γ(x) = t
Γ[x->tx] |- e_0 : t_0 / Γ |- fnπ x=>e_0 : t_x -> t_0 (x类型是t_x,e_0最后输出类型是 t_0)
Γ[f -> tx->t_0][x->t_x] |- e_0 : t_0 / Γ |- funπ f x=>e_0 : t_x -> t_0 (x类型是t_x,e_0最后输出类型是 t_0,递归时,f作为t_x进入以t_0输出)
Γ |- e_1 : t_2 -> t_0 Γ |- e_2 : t_2 / Γ |- e_1 e_2 -> t_0 (e_1将t_2类型转换成t_0,e_2是t_2类型。最后输出是t_0类型)
Γ |- e_0 : bool Γ |- e_1 : t Γ |- e_2 : t / Γ |- if e_0 then e_1 else e_2 : t (经过判断后执行语句)
Γ |- e_1 : t_1 Γ[x -> t_1] |- e_2 : t_2 / Γ |- let e_1 in e_2 : t_2 (最终根据e_2确定type)
Γ |- e_1 : t_1 Γ |- e_2 : t_2 / Γ |- e_1 op e_2 : t (判断语句两个参数是可以比较的类型,返回值是bool类型)
例子 Example
首先let in结构Γ |- e_1 : t_1 Γ[x -> t_1] |- e_2 : t_2 / Γ |- let e_1 in e_2 : t_2
fun 结构Γ[f -> tx->t_0][x->t_x] |- e_0 : t_0 / Γ |- funπ f x=>e_0 : t_x -t_0
fn结构Γ[x->tx] |- y : t_0 / Γ |- fn\π x=>y : tx -> t_0 Γ[x->t_x] |- z : t_0 / Γ |- fnπ x=>z : t_x -t_0
e_1 e_2结构 Γ |- e_1 : t_2 -> t_0 Γ |- e_2 : t_2 / Γ |- e_1 e_2 -> t_0
总结下来的操作就是 [f -> (t -> t) -> (t -> t)] [x -> t ->t] 递归函数中,不断循环fn y的操作,再执行fn z的操作。
所以基于类型的系统模型应用在控制流分析中可以根据数据类型调用函数,int bool始终是本身,t->t代表是一个函数的抽象。
由于存在多个相同的类型转换的函数抽象无法区别彼此,我们添加标记φ。
我们在之前的fn和fun结构中增加了断点,此时可以应用这些断点进行区别。
基于响应的系统模型Effect System
对于特定type_1和特定type_2形成对应关系的语句,我们应当作出相应的特定操作。这就是基于响应的思想。
对于控制流,我们要做的响应是抽象函数的调用。对于异常,我们要做出不同特定的响应。对于作用域我们要对数据作用域作出响应。对于交互我们要对不同时间的信号作出响应。
要实现这样一个系统模型,我们要使用基于类型的函数语言,底层类型系统,响应系统的拓展。
首先基于类型的函数语言和底层类型系统在上面已经提到,响应系统的拓展就是使用上面提到的φ进行。
上一个例子我们得到 [f -> (t -> t) -> (t -> t)] [x -> t ->t]的结论,但是转换之间调用的函数无法确定,此时我们应用φ。
由于存在fn y和fn z,所以同类φ中存在y z 两种方法,实际执行中可能是两种之中的一个。还有fun f,同类φ中只有F。至于g ()则不调用函数,为空。
最后得到 [f -> (t – {Y,Z} -> t) – {F} -> (t – 空 -> t)] [x -> t – {Y,Z} ->t]
仅仅记录调用函数肯定不能直接实现程序分析,还要有值,也就是程序中一定存在某处是赋值语句,在控制流分析中,我们把赋值语句也当作了函数,或者说某个函数的返回值是一个值,所以我们可以做出e -> v 的归纳。
加上这一归纳后的语法也发生了一些变化:
c -> c
fn_π x => e0 —> fn\π x -> e_0
fun_π f x -> e0 —> fn\π x ->(e0[f -> fun\π f x -> e_0]) (在递归过程中,不断分解成fn x -> e_0)
e_1 —> fn_π x -> e_0 e_2 —> v_2 e_0[x -> v_2] —> v_0 / e_1 e_2 —>v_0 (e_1是一个函数,e_2是赋值,最终是将v_2当作x代入函数,返回值v_0)
e_0 —>true e_1 —>v_1 / if e_0 then e_1 else e_2 —> v_1 (判断为true返回e_1的返回值)
e_0 —>false e_2 —>v_2 / if e_0 then e_1 else e_2 —> v_2 (判断为false返回e_2的返回值)
e_1 -> v_1 e_2[x->v_1] ->v_2 /let x = e_1 in e_2 ->v_2 (函数返回值为v_1 代入e_2中得到v_2)
e_1 —> v_1 e_2 —> v_2 / e_1 op e_2 — v (v_1 op v_2 = v)
依旧是上面的例子
let in结构g为fun返回值
—> fun_F f x => f (fn_Y y => y) fn_z z => z
—>递归函数为 fn_F x => ((fun_F f x => f (fn_Y y => y)) fn_Y y => y)
—> v g返回值为v
推理算法 Inference Algorithms
明确了模型,接下来我们要选择算法实现模型。
首先,对于类型而言,除了明确定义与常数的类型确定,有些函数或语句的返回结果无法确定,所以在实际运用中,我们添加α用来表示这些类型的集合,对于一个返回值,我们与α一个类型建立映射。而这个类型我们用断点去命名。
虽然表示了类型,但是类型依旧不能明确,所以需要通过上下文加以限制从而使用算法去判断数据类型。因此我们增加新的语法:U
U是用于建立上下文联系的工具,对于U(int,int) 和U(bool,bool),我们保持原有id集合记录类型,对于U(t_1 -> t_2 , t’_1 ->t’_2)记作θ_1 o θ_2 。θ_1要满足θ_1 t_1 -> θ_1 t’_1 θ_2要满足θ_2(θ_1 t_2) ->θ_2(θ_1 t’_2)。即要想t_1 -> t_2 , t’_1 ->t’_2等价,需要满足t_1和t’_1存在映射, t_2和t’_2存在映射,最终实现 t_1 -> t_2 和 t’_1 ->t’_2存在映射。而映射关系就是θ_1 o θ_2。对于U(α , t) 和U(t , α)则需要α 是 t 或者 α 是 t没有表示的类型。记作[α -> t]
例子
U(a -> a,(b -> b) -> c)
存在θ_1满足a和b->b存在类型映射,θ_2满足a和c存在类型映射。除此之外,还需要b -> b和c存在类型映射关系,即[a|-> b->b] [a |-> c] [c |-> b->b]
接下来我们对所有语句类型进行语法描述
W(Γ , c) = (t_c ,id) 对于常数 c ,数据类型为 t_c 保存在 id集合中
W(Γ , x) = (Γ(x) ,id) 对于变量 x ,数据类型为 Γ(x) 保存在 id集合中
W(Γ , fn_π x => e_0) = let α_x be fresh (t_0 ,θ_0 ) = W(Γ[x->α_x] , e_0) in ((θ_0,α_x) -> t_0 , θ_0) 对于函数fn ,将 x 的数据类型先设为空,判断e_0语句中变量的数据类型,和 x 建立映射,保存在θ中。
W(Γ , fun_π f x => e_0) = let α_x α_0 be fresh (t_0 ,θ_0 ) = W(Γ[x->α_x -> α_0][x -> α_x] , e_0) θ_1 = U(t_0,θ_0,α_0) in (θ_1(θ_0,α_x) ->θ_1 t_0 , θ_1 o θ_0) 对于递归函数fun f,将 x 和输出的数据类型先设为空,判断e_0语句中变量的数据类型,和 输出 建立映射,保存在θ_0中。将 x 和输出进行复制保存在θ_1中。
W(Γ , e_1 e_2) = let (t_1, θ_1) = W(Γ,e_1) (t_2, θ_2) = W(θ_1 Γ,e_2) α be fresh θ_3 = U (θ_2 t_1,t_2 -> α ) in (θ_3 α,θ_3 o θ_2 o θ_1 ) 对于e_1 e_2 ,将 返回值 的数据类型先设为空,判断e_1 e_2语句中变量的数据类型,和 返回值 建立映射,保存在θ_3 o θ_2 o θ_1中。
W(Γ , if e_0 then e_1 else e_2) = let (t_0, θ_0) = W(Γ,e_0) (t_1, θ_1) = W(θ_0 Γ,e_1) (t_2, θ_2) = W(θ_1(θ_0 Γ) ,e_2) θ_3 = U (θ_2(θ_1 t_0),bool ) θ_4 = U (θ_3 t_2,θ_3(θ_2 t_2) ) in (θ_4(θ_3 t_2) , θ_4 o θ_3 o θ_2 o θ_1 ) 对于if,判断e_1 e_2语句中变量的数据类型,根据e_0选择e_1 或 e_2和 返回值 建立映射,保存在θ_4 o θ_3 o θ_2 o θ_1中。
W(Γ , let x = e_1 in e_2) = let (t_1, θ_1) = W(Γ,e_1) (t_2, θ_2) = W((θ_1 Γ)[x->t_1,e_2) in (t_2 , θ_2 o θ_1 ) 对于let in ,判断e_1 语句中变量的数据类型,代入到e_2中判断返回值数据类型,保存在 θ_2 o θ_1中。
W(Γ , e_1 op e_2) = let (t_1, θ_1) = W(Γ,e_1) (t_2, θ_2) = W(θ_1 Γ,e_2) θ_3 = U (θ_2 t_1,t_op ) θ_4 = U (θ_3 t_2,t_op ) in (t_op,θ_4 o θ_3 o θ_2 o θ_1) 对于e_1 op e_2 ,判断e_1 e_2语句中变量的数据类型,建立类型映射保存到到θ_4 θ_3中 ,将t_op保存在θ_4 o θ_3 o θ_2 o θ_1中。
上面是基于类型的系统模型的算法语法,接下来是基于响应的系统模型。
对于响应系统的拓展,我们用β表示响应集合,用数字区分各个响应。和上面语法类似,我们要建立类型统一:对于U(int,int)和U(bool,bool)没有区别,对于U(t_1 -β-> t_2,t’_1 -β‘->t’_2 ),除了之前的t_1和t’_1 ,t_2和t’_2存在映射外,β和β’也要存在映射。
例子
U(a -1-> a,(b -2->b) -3-> c)
1和3存在映射 [3 |->1]
其余和基于类型的结果一样[a |-> b-2->b][c |-> b -2-> b]
最终得到[3 |->1][a |-> b-2->b][c |-> b -2-> b]
除此之外,我们1 ,2,3进行约束,即与实际建立联系。
例子
(fn_X x=>x) (fn_Y y=>y)
对于上面的例子,我们可以抽象成a -1-> a,(b -2->b) -3-> c
其中,我们将1和X建立联系,2和Y建立联系。从而明确调用内容。
最后我们对之前的例子完整应用上面的算法。
对于let in结构,我们直接将g替换
(fun_F f x => f (fn_Y y => y)) (fn_Z z=>z)
对于(fun_F f x => f (fn_Y y => y))我们可以抽象成g |-> (a -2-> a) -1->b 其中1是F 2是Y
对于(fn_Z z=>z)我们抽象成c -3-> c -4->d
(fun_F f x => f (fn_Y y => y)) (fn_Z z=>z)是 e_1 e_2的结构,所以存在类型匹配,即 a -> c b ->d 1->4 2->3
所以4包含F,3包含Y,同时由于3本身是fn_Z z=>z,所以3包含Z
也就是这一段代码我们可以简化成 (a->a) ->b,其中 a->a的处理机制2和3,也就是YZ机制,->b包含F机制和输出机制。
最后
欢迎指教
DR@03@星盟


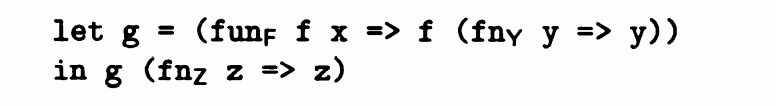







发表评论
您还未登录,请先登录。
登录