在上一篇文章中,我们探讨了如何将输入和输出表示为向量,以及一个训练好的深度神经网络,是如何根据一张照片来判断其中是不是一只猫的,也就是推理过程。接下来,我们开始进入另一个话题,即神经网络是如何训练的?
为此,我们需要明确两件事情。第一件事是,训练啥?第二件使其,咋训练?好了,我们下来讨论第一个问题。
训练啥?
首先,我们需要明确一件事情,那就是当我们说训练神经网络时,一般已经确定了以下事项:
- 选用哪种神经网络的架构?比如,选择的是卷积神经网络,还是循环神经网络,等等。
- 神经网络中含有几层?
- 每层中含有多少神经元?
- 各个层之间的神经元如何连接?
- 各个神经元使用什么样的激活函数?
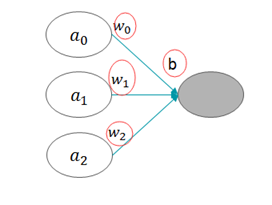
如您所见,既然这么多因素都已经确定下来了,那么,还有哪些需要我们进行磨合的呢?那就是激活函数的参数,包括两部分:
- 权重w
- 偏置项b
图1 训练网络时需要调整的权重w和偏置项b
为了突出显示需要调整的这两部分,我们可以把我们的函数表达式更新为:
其中,Θ表示神经网络所需的所有参数,即权重和偏置项。也就是说,用于表示神经网络的函数f的输入内容,不仅需要照片本身,而且还需要神经网络的参数。
到目前为止,我们介绍了训练神经网络时,到底要训练哪些内容,即权重和偏置项。那么,接下来我们再来说说如何训练它们。
如何训练?
我们已经明确了训练网络的目标,那就是找到合适的参数。那么,如何寻找这些合适的参数呢?众所周知,做事情的方式有两种,一种是一步到位,另一种是循序渐进。而训练网络参数的方式,就是属于后者。
当然,训练神经网络的思路并不复杂,比如,以监督式训练为例,首先给权重和偏置项(Θ)随机赋值,然后,拿一个训练样本(如一张照片)喂给神经网络,这时,我们就得到一个输出向量。接下来,我们可以分析输出结果与预期结果之前的差异了。通常情况下,我们会用成本函数来衡量参数的表现到底有多么“烂”,其表达式如下所示:
或者:
其中,C表示成本函数;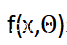
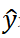
成本函数的值越大,说明参数Θ 该值越小,说明参数的表现越好。所以,如果成本函数的值大于某个阈值的话,我们就需要对神经网络的参数进行相应的修改;重复该过程,直到找到令成本函数的值低于特定阈值的参数为止。当然,我们不可能每训练一个样本就调整一次参数,因为这样太过麻烦了;相反,我们可以采取其他方式,比如训练一批样本后调整一次参数,等等。
前面说过,成本函数本质上就是衡量参数的表现到底有多么“烂”的,但是,它到底是怎么衡量的呢?实际上,这里可用的方法也很多,比如,常见的一种方法是先求预期输出与实际输出之差,然后,再取平方。这样的话,实际输出与预期输出之间的差别越大,成本函数的输出也越大,并且这种“大”是非线性的,因为进行了平方运算——换句话说,这时的参数 将会遭受更大的惩罚。
下面是单个训练样本的成本计算公式:
其中,其中:当i表示正确的目标标签的索引时,的值为1,否则,其值为0。因此 ,我们的成本函数可以表示为:
例如,假设我们在训练期间将一张小猫的图片输入到神经网络中,其输出向量如下所示:
我们假设该图片的正确标签是“猫”,对应于矢量中的第二个值。理想情况下,这个预测值应该非常接近1,而不是目前的值0.127。如果网络训练状况良好的话,它应该返回类似下面这样的预测向量:
对于这个样本的预测成本计算过程为:
就本例来说,我们发现对小猫进行分类的成本是很高的。因此,我们需要继续调整网络中的一些参数,以进一步降低成本。
然而,在评估神经网络的分类效果时,当然不能只看单个训练样本的成本,而是要综合考虑所有训练样本的总体成本。一般来说,我们可以使用平均成本来衡量神经网络的整体性能,比如,计算所有样本的误差的平方的平均值,也就是所谓的均方误差(MSE)。
一般来说,用于计算平均成本的函数,一般称为损失函数。当然,损失函数可以使用不同的算法来计算训练过程中的损失。对于分类模型来说,通常会使用分类交叉熵损失函数,因为这个函数能更好地惩罚网络返回的较高置信度的误差。
梯度下降法
前面说过,为了改进神经网络的效果,我们就需要调整其权重和偏置,以便让平均成本变得尽可能小。换句话说,就是对Θ所代表的参数进行调整,使得函数f对于所有训练样本的平均误差最小化。那么,我们该如何调整呢?通常情况下,我们可以求助于梯度下降法。
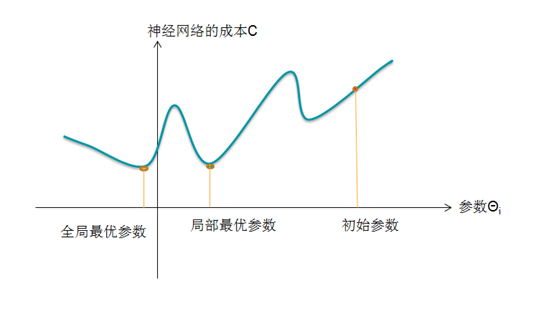
为了帮助大家理解梯度下降,我们需要对神经网络进行简化:假设网络中只有一个可调参数Θi,而不是有成千上万个可调的参数。这样的话,我们就可以通过下图来表示参数与损失函数之间的关系了:
图2 训练网络时,可利用梯度下降法寻找令网络成本最小的参数
在上图中,x轴对应于可调参数。给定x的值,我们就可以用选择的损失函数(如MSE)来计算神经网络的平均成本。当然,为了便于可视化,参数轴已经被极度简化了——现实中,表示参数的轴应该有成千上万个,因为每个参数对应一个轴,而每个网络通常都有非常多的参数。
此外,我们可以看到,损失函数的曲线存在某些局部最小值,它对应的参数,就是神经网络的局部最优参数。在使用梯度下降法时,最初可以随机选择一组参数,然后,计算在该组参数下神经网络的损失函数的值,并顺着损失函数梯度下降最快的方向,找到这些最优参数。
稍微具体点讲,反向传播算法可以在深度神经网络的训练阶段,自动确定需要更新哪些权重和偏差以及具体更新多少。那么,为什么叫“反向传播”呢?很简单,这是因为在调整网络参数的过程中,输出层的损失将通过神经网络从后向前传播。
当然,反向传播的数学原理还是很复杂的,这里我们就不深究了。但是,有一点需要了解,那就是它不仅可以用来训练神经网络,还能用于优化对抗性样本的生成。所以,我们后面只要知道如何去用就可以了。
小结
在本文中,我们为读者介绍了神经网络训练过程相关的两个问题:到底训练的是什么?以及如何进行训练?同时,我们还单独介绍了一种非常常见的训练算法:梯度下降法。实际上,梯度下降法,不仅可以用于训练神经网络,而且还可以帮助我们生成对抗性样本。在下一篇文中 ,我们将用Python来实现一个简单的神经网络。


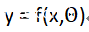
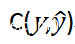
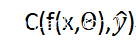
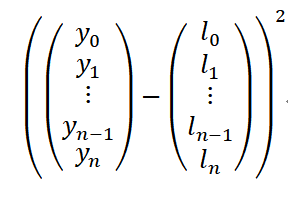
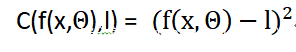
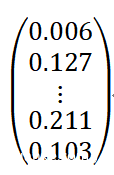
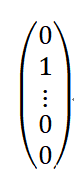
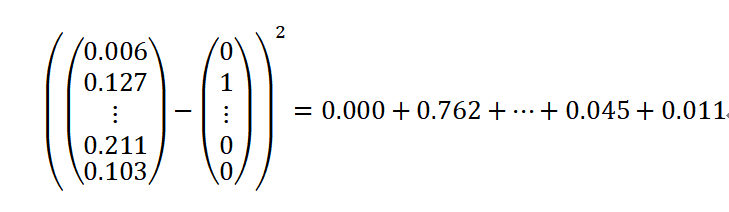







发表评论
您还未登录,请先登录。
登录