上一篇内容中我们引入了多路径探索、模式更新等内容,这次我们会引入新的思路,并且尝试特定路径上的搜索。
首先要明确一点,因为上一篇中我们引入了“现有模式变异后不仅仅作为fuzzing输入,还作为新加入模式”这一重要的观点,所以我们在提到模式变异时,不单单要考虑作为输入的问题,也要记得它是新加入的模式。
函数级别与函数距离
在之前文章中,我们思考的往往是代码级别的问题,比如代码覆盖率,就是看我们走过了多少代码,但实际上,我们操作时经常会把粒度放大到函数级,以函数(这里的提到的函数都是用户级的函数)之间的关系来思考问题,来看个例子:
my_input()
用户 = verify()
if 用户 == asa9ao:
flag()
else:
byebye()
对于这样的代码,不管是软件测试或者搞安全的,第一反应其实都是去找函数调用处下断点,一旦程序运行到了我们想找的函数,后面基本上就是阳关大道了,而对于函数里面具体的代码我们反而不是很关心。这样的思维带来了两大好处:
- 程序的逻辑结构更加清晰。几千行的代码可能只有十几个函数,逻辑上一下子就简单了。
- 测试上方便简单,原本几千行代码你需要“平等”对待,现在你可以先测函数,没问题的函数丢一边,有问题的找到对应函数里的代码再进行“重点照顾”。
可以看到,粒度变大后,实际上就类似“分组”的概念,组间先进行操作,组内后操作,如果遇到非常简单,一个函数写到底的代码,我们也可以把它当作一个组,再组内测试即可,实际上就退化为了我们前几篇文章所讲的情况。我们可以将之前代码级别的概念,全都放在这个组内操作。
说了这么多,函数之间我们又该进行哪些操作呢?首先,代码级别的概念我们可以统统继承过来:
- 代码覆盖率变为函数覆盖率,调用了多少代码改为调用了几个函数
- 路径执行频率中的路径统计的不再是代码,而是函数
当然你可能会说,那会不会有人写代码,重点代码不写几个函数,反而是不重要的代码函数一堆呢?首先正经人写代码肯定不会这么写,其次我们在Lv3文章中已经让我们的代码获得了多路径探索的能力,实际上我们在函数层面是一样的,我们仍然会是每个路径的调用都处于一个水平线上,所以并不会有什么影响。
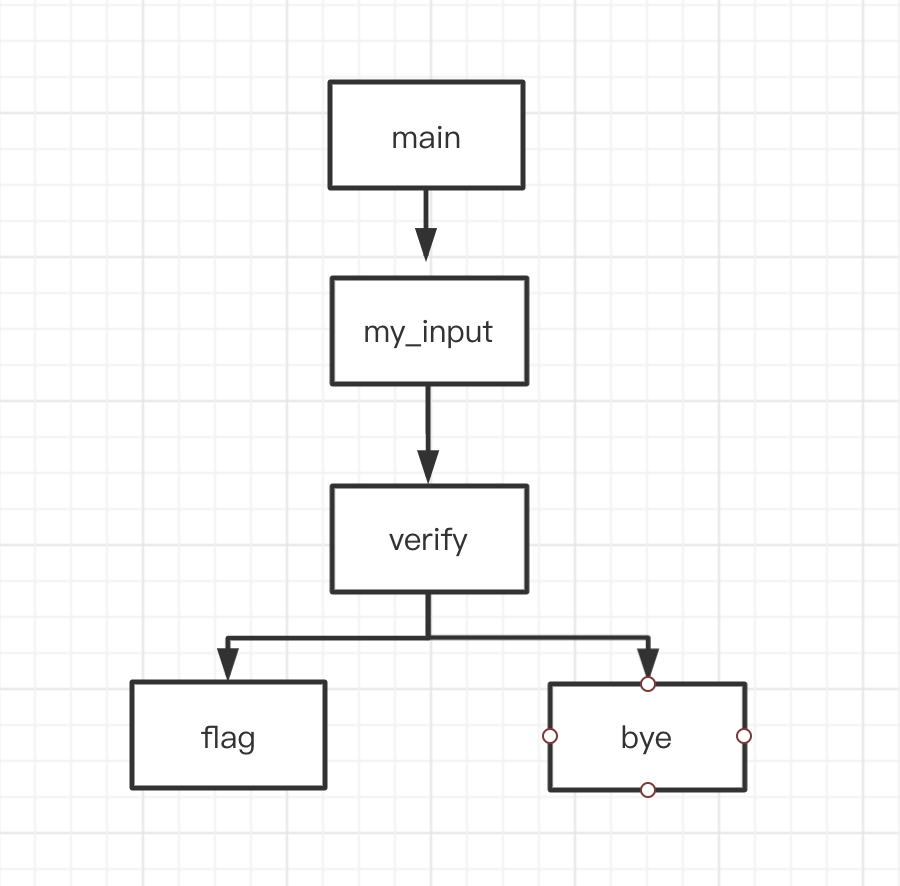
此外,由于函数级别逻辑结构简单了,我们就可以计算一些新玩意了——函数距离。下面的图片中展示了上面程序的函数调用图:
我们假设我们要找的函数是flag,我们已经走到了verify,那我们的函数距离就是1,而对于flag和bye这俩函数,因为没有路径连接他俩,所以我们可以直接设置为-1或者其他值,表示不可能到达即可。这样我们就可以定向计算我们所处的位置与目标位置的距离了。
那么有同学就会问了:为什么我们不在代码级别计算呢?其实很简单——麻烦。我们假设我们要找的代码是bye中的某一行printf,假设verify有1000行代码,我们在每一步都计算一次的话就要储存1000个距离,而显然这里面大部分的距离都是重复且无效的。
那么又有同学要问了:代码级别的覆盖率什么的都好说,我们得到源代码后就可以直接算了,函数级别咋整呢?其实我们在Lv3中就完成了这些工作了!我们利用ast能够获得每一句代码的node,而node中on_functiondef就是函数的开头,我们只需要对上一篇文章中提到的cfg技术进行略微的改进就可以计算函数距离了。
我们接下来就把函数距离引入我们的调度器,让调度器可以进行指定函数的探索,我们先来定义模式距离的概念:
i表示模式,t表示目标函数,s表示函数,|CG|是所有节点的数量,我们再计算模式的energy就可以使用这个了,下面是fuzzingbook的代码:
def assignEnergy(self, population):
for seed in population:
if not hasattr(seed, 'distance'):
num_dist = 0
sum_dist = 0
for f in self.__getFunctions__(seed.coverage):
if f in list(distance):
sum_dist += distance[f]
num_dist += 1
seed.distance = sum_dist / num_dist
seed.energy = (1 / seed.distance) ** self.exponent
其中,sum_dist就是保存了f的距离,而num_dist就代表了CG图中所有节点的数量,最后用了类似我们上一篇文章的反函数来得到energy,其中的exponent依然是可以调整的参数。
但是上面的想法显然是有“漏洞”的,因为距离这个东西本身是没有限制的,我们可以假定它的取值范围是0到无穷大,这里的无穷大不代表不能到达,而是我们的距离却是是存在要多大有多大的情况,这种情况下,我们的energy会由于“贫富差距”过大,而导致有些合法的路径“饿死”了。比如,按照我们上一篇文章的概率计算方式,因为energy差距过大,会导致概率向energy大的一方严重倾斜,即使不被饿死,也和我们的初衷相悖,所以我们可以再简单处理一下:
公式看着复杂,实际上就是简单的进行了归一化,将d的范围锁定在了0-1的范围内。fuzzingbook中给出了一个迷宫的例子,因为涉及代码过多,就不再演示了,实际跑一下会发现,经过我们的操作,效率大大提高。
广义距离与搜索空间
有了上面的距离,我们可以找到模式与我们想要的目标之间的“差距”,而有了这个距离我们能不能有更好的方法去探索呢?如果你曾经接触过数学建模或是机器学习的知识,那你一定可以想到,我们可以利用优化的思路解决问题,我们把距离看作是loss,我们来优化模式,假设模式是由参数组成的,我们调整这些参数,计算出loss,通过改变我们的模式,不断的降低loss,最终找到loss为0的模式,也就找到了通往目标的大道。当然,这里的距离是可以根据情况具体设置的,只要可以体现与目标之间的差距即可。
我们来看fuzzingbook给出的例子:
def test_me(x, y):
if x == 2 * (y + 1):
return True
else:
return False
这里我们假设要探索的目标是True,这里我们为了简单期间,我们直接把输入的数当作模式,不进行模式的变异,而距离由于它是判断两个值是否相等,我们可以进行简单的移项,得到x -2 (y + 1)是否等于0,那么loss我们就可以直接视作是x -2 (y + 1)的绝对值即可。我们随机用两个数,比如2和4,很自然就可以算出,loss为8,那么下一步我们就可以进行优化了。
首先我们定义一个搜索空间的概念,其实就是模式的“变异”范围,你可以认为模式能够进行1000次变异,那么这1000次变异组成的所有模式就都是你对于这个模式的搜索空间了,当然,这也需要根据实际情况调整,比如我们的例子中,输入就是两个数组成的元组,那么我们就可以认为,这两个数的相邻的1000个数自由组合,组成的1000*1000个元组就是我们对于这个模式的搜索空间。每个模式的搜索空间加起来,就得到了我们总体的搜索空间,当然,为了搜索空间不会无限膨胀下去,一般我们也会设置搜索空间的边界,比如这个例子中我们可以设置x不超过1w。
def neighbours(x, y):
return [(x + dx, y + dy) for dx in range(-500,500)
for dy in range(-500,500)]
接下来我们就在搜索空间上进行优化了,有一种著名的方式叫做Hillclimbing算法,我们可以把我们的搜索空间想象成地面,把损失想象成“高度”,搜索空间无数的“高度”就组成了一个山峰,我们随机生成的点就在山峰的一个点,我们环视四周,找到第一个比现在低的地方,我们就去到那个点,持续这个过程,我们的loss就会不断降低。
def hillclimber(x,y):
loss = get_loss(x,y)
while loss > 0:
iterations += 1
for (nextx, nexty) in neighbours(x, y):
new_loss = get_loss(nextx, nexty)
if new_loss < loss:
x, y = nextx, nexty
loss = new_loss
break
print(x, y)
当然,这样的思考是有问题的,你可以想象这样的情况:
- 你在山上,看看周围,发现右边就比现在的地方低,于是你去了右边,你不停的往右边去,结果最终右边泥石流,下不了山,困住了;左边虽然看起来是比现在高一些,但是向左爬一会后是个悬崖,你直接跳下去就完事了。
- 你一步步的看,看到哪走哪,最终走了好久才下山;别人拿望远镜,一下子就找到了视野范围里最低的路径,每次直接走到那
第一个问题我们其实是没有很好的办法解决的,我们只能说是找到一个相对最优解,或者尽可能避免这种情况的出现,但对于第二个问题就很好解决了,我们只需要把上面代码中的break去掉。去掉之后,我们代码的语意就变成:环顾搜索空间,找到搜索空间里最低的点。这种方法能有效的提高效率,并且在一定程度上可以避免第一个问题,因为第二种方法有了“大局观”,不再是傻乎乎的走了。
我们用cgi_decode()(Lv2中可以找到)的例子来看看,他要求我们输入一个字符串,并对字符串进行解析,对于字符串,我们就可以使用变异的手段来定义搜索空间了
def neighbour_strings(x):
n = []
for i in range(0,1000)
a = mutate_limit(x,i)
n.append(a)
return n
简单起见,我们这里假设变异就只有就只有字符的更改,没有长度变化,而搜索空间的限制就是字符得是在ascii范围内合法的。
那么问题又来了,我们之前探索的路径是==,这非常简单,我们简单的移项后就得到了优化的目标,像是>=这种比较复杂的我们该怎么办呢?其实也很简单,我们下面就逐个说一下:
- ==和!=,实质上一样,True我们使用abs(a – b)即可,False我们使用1
- 大于、小于实质上一样,对于True使用大 – 小 + 1,对与False使用小 – 大即可
- 大于等于、小于等于本质上一样,True就是大 – 小,False就是小 – 大 + 1
为了以后方面使用,我们可以原子化的思想,借鉴Lv3中抽象语法树对于词的拆分,将要评价的目标拆为:左项、比较符、右项,
def evaluate_condition(num, op, lhs, rhs):
distance_true = 0
distance_false = 0
# 这是展示的==操作
if op == "Eq":
if lhs == rhs:
distance_false = 1
else:
distance_true = abs(lhs - rhs)
# 写其他的操作
if distance_true == 0:
return True
else:
return False
那如果出现了像是if a==b and b==c这种多条件的情况怎么办呢?其实也很简单:
- and,说明两种情况都得成立才行,那我们就选择两种情况中最大的作为距离即可
- or,说明两种情况成立一种即可,有两种思路
- 短路,因为两种都可以,我们就只关心第一种
- 选择两种中的最小的作为距离
- in,判断a是否在b里,实质就是对b中的每一个元素都进行了or操作,所以我们相应的求出b中每一个元素的距离,选择最小的即可。
我们按照上面思路书写代码,即可完成对cgi_decode的测试。
看上去很美好是吧,但是很抱歉,还是有问题,你所看到的美好都是我们假设出来的,这山是我们玩的“假山”,我们假设输入的字符不是ascii,而是utf-8的呢?我们运用改进的Hillclimbing时,是每走一步都要去看周围所有的搜索空间中谁最低,相当于对每一个模式都去开辟了一个搜索空间,一旦搜索空间的单个面积大了,这玩意加起来的消耗我们可接受不起。那我们还有办法吗?说实话,没有完全的办法,我们只能是使用一些讨巧的方式减少消耗:
- 限制迭代,简单说就是限制你下山走的次数,你走10步下不来就下不来吧,咱直接说再见。
- 找路时只看一部分,不全看,比如本来走一步要开辟100×100的空间,那我不开了,我就开10个,我就选10个里面最小的走。这其实就是把我们改进后的Hillclimbing又改回去了,算是一种折中方案
- 掷骰子,我随机选一条路,看能不能走,能走就走,不能走就不走接着随机。这是一种非常讨巧的方法,完全规避了搜索空间庞大的问题,甚至不用求搜索空间,只用求随机出来的模式的距离即可。代码就更好写了,用我们现成的变异函数即可,每次选路时进行一次变异,变异的距离小,就走这个。
上面都是对Hillclimbing算法的改进,但无论怎么改,我们还是没法从本质上改善算法的缺陷,最好的方法就是换方法,我们选个别的算法来进行优化。
fuzzingbook上给我们介绍了一种遗传算法来解决问题,其关键函数长这样:
def crossover(parent1, parent2):
pos = random.randint(1, len(parent1))
offspring1 = parent1[:pos] + parent2[pos:]
offspring2 = parent2[:pos] + parent1[pos:]
return (offspring1, offspring2)
函数很简单,把俩字符串拆开,各挑一部分再拼起来。实际上这是在模拟遗传的过程,我们的字符就相当于基因,字符串就是染色体,在繁殖后代时,父母会各自给后代一部分的染色体。
那么父母是怎么来的呢?很简单,物竞天择,适者生存。我们先随机生成一部分字符串,选择其中loss(别忘了loss就是上面求的距离)最小的一部分,让他们进行“繁殖”,模拟优秀基因的传递过程,这样,通过把优秀基因不断的传递下来,我们的字符串的loss就会越来越低。
当然,生物学告诉我们,新的性状不会凭空产生,都是基因变异的结果,这个过程中我们同样需要考虑基因变异的问题,因为纯粹的遗传,基因没有发生改变,就无法产生新的字符,我们可以使用我们的变异函数,按照一定的概率对基因进行变异,创造出新的基因。
说了这么多,其实本质就是通过降低loss函数,不断优化我们模式的问题。大家可以自由发挥,甚至可以把机器学习、数学统计那部分模型拿过来用,只要是能降低loss,那就是好方法。
总结
这一章开始,体现了大量的知识“联动”,我们一种知识可以放在不同的地方发挥作用,一个概念也可以“两开花”,我们学到的不仅仅是fuzzing,也是对计算机问题的处理思路。
下一篇开始我们将开始新征程,跳出现在的思维,让我们的fuzzing史莱姆更加强大。


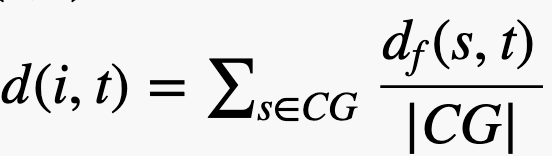
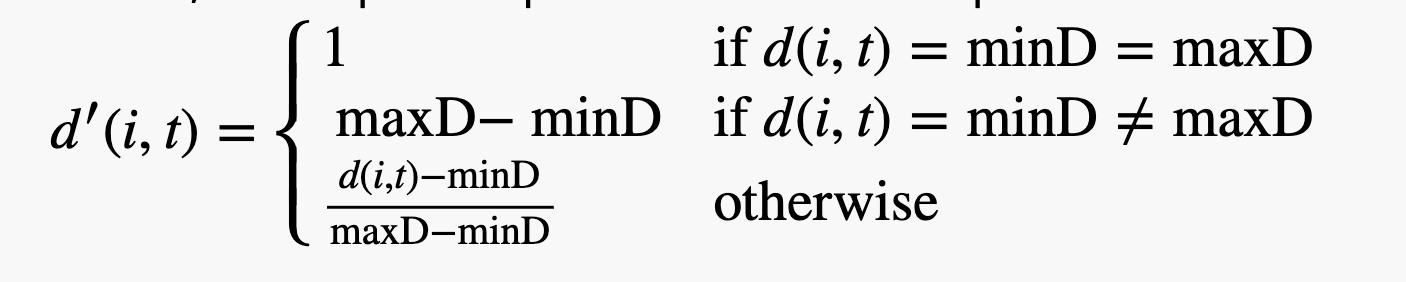







发表评论
您还未登录,请先登录。
登录