我们之前的fuzzing往往考虑的都是一个字符串,绞尽脑汁让这个字符串的字符发生变化进而提高某些指标,我们这次把段位上升,不在局限于怎么“美化”句子,而是如何“定义”句子。
还记得最初我们用的bc吗?如果你一味使用Lv4之前的技术,那你其实永远都是在“乱搞”,因为它其实有一套自己的逻辑,如果找到了逻辑你可以绝杀,就像是玄幻小说,掌握规则的人永远比普通修炼的牛,我们也要让我们的史莱姆掌控法则。
语法
我们说话写字都是有一定规则的,编写程序是这样,写数学公式也是这样,现在我们来想想到底是什么“限制”了我们呢?
- 首先当然是范围,你也可以理解为集合当中说的定义域,简单说就是规定哪些符号你能用,哪些不能用,以只包含加减乘除的小学数学表达式为例,我们的定义域就限制在了加减乘除四个符号以及0~9十个数字罢了,你用了a你就是错了,就不是一个合格的表达式了。
- 其次我们可以想到,是一组规则让我们不能乱写。小学数学表达式可不会出现1++这种奇奇怪怪的式子,这就说明背后有一套规则约束,而这套规则还应该是支持无限写下去的,因为按道理来说,你可以写1+1+1+···一直写下去。
如果让我们用一套规范点的方式去概括这两个方面呢?范围我们很好解决,我们可以用正则表达式来检测,不符合规则淘汰就是了,第二点我们该如何做呢?其实我们大学就学过这个问题,这其实就是个有限状态机。
所谓有限状态机,其实就是一组“状态”,它们之间互相能够进行转换。比如Linux的进程状态,那有人就要问了,你刚说了1+1+1+能无限写下出,怎么这会反而有限了呢?其实有限说的是状态是有限的,比如Linux的进程状态,满打满算就五个,但是一个进程你完全可以无限次的经历这些状态。
这两点就组成了我们的语法,我们只需要按照一定的规则,就可以轻松写出对应的语法,比如
<start> ::= <digit><digit>
<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
首先是个start标签,标志着开始,::=这个符号表示前者可以由后者代替,而|就代表or的意思,所以上面的语句就代表,以两个数字开头,后面啥也没有,其实就是我们需要写两个0-9的数,比如00,比如12。
那你就要问了,我要是写1000个数你咋整啊,我总不能写1000个<digit>吧?其实也很简单,加一句话就完事了
<start> ::= <integer>
<integer> ::= <digit> | <digit><integer>
<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
我们引入了递归的概念来处理这个问题,用递归达到无限循环的目的。直接来看,首先我们以integer开头,而integer可以是数字,也可以是数字然后再来个integer,这就可以一直递归下去了。比如我写1,可以吗?可以,integer=digit=1即可;写23,可以吗?可以,integer=3iteger,再处理第二个integer=3即可,就得到integer = 23,这样我们就轻松实现了无限的概念。
那又有问题了,我如何表达我的数有正负呢?也简单,在状态转换的位置加入限制即可,如下
<start> ::= <number>
<number> ::= <integer> | +<integer> | -<integer>
<integer> ::= <digit> | <digit><integer>
<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
假设我们输入的是-3,那么就是number=-integer,integer=3,number=-3,完毕。
有了上面几个例子,相信你已经会利用“解包”的思想读这些语法了,我们每次读时,如果有还不清楚的位置,那就先带着标签,然后一步步把标签给去了,这就是解包的思想,我们不仅仅读需要这种思想,写代码实现也要如此。下面我们就尝试写代码,让程序按照我们定的规则来说话。
DIGIT_GRAMMAR = {
"<start>":
["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"]
}
我们用字典存储标签即可,而对于生成的过程如下:
term = start_symbol
expansion_trials = 0
while len(nonterminals(term)) > 0:
symbol = random.choice(nonterminals(term))
expansions = grammar[symbol]
expansion = random.choice(expansions)
new_term = term.replace(symbol, expansion, 1)
if len(nonterminals(new_term)) < max_nonterminals:
term = new_term
if log:
print("%-40s" % (symbol + " -> " + expansion), term)
expansion_trials = 0
else:
expansion_trials += 1
if expansion_trials >= max_expansion_trials:
raise ExpansionError("Cannot expand " + repr(term))
nonterminals函数用来找非终端的标签,对于能够继续产生标签的标签,我们叫它非终端,比如start;对于只能产生最终结果不能继续生成标签的标签,就是终端,比如digit。
因为我们是一步步解包,所以首先我们得有包,他其实就是在检查当前的term是不是有包,如果有包的话,就在包里随机找一个,然后再从包中找一个标签,我们就到了新的表达式,当然,为了这个过程不会无限循环下去,我们人为定义了循环的最大值,让他不会无限循环。
这样说可能有点抽象,我们举个例子,就用我们的正负数来说:
- nonterminals找到非终端的值,一开始就是number(节省篇幅,跳了start标签)
- 随机选一个作为expansions ,这里只有number
- 随机在number对应的里面选一个,假设选到了+<integer>
- 那么新标签现在就是+<integer>
- 找所有非终端的值,只有<integer>
- 随机选,只能选<integer>
- 随机在integer对应的里面选一个,假设选中了<digit><integer>
- 那么新标签现在是+<digit><integer>
- 重复….
如此,我们就可以生成我们语法要求格式的字符串,同时我们也可以直观看到,如果不限制循环的次数,他完全可以-1111···这样一直生成下去。解包的思想在这里发挥了重要作用。在Fuzzingbook还给了很多例子和如何将这种语法封装为工具箱,因为篇幅限制就不再是详述了,大家可以自行参考。
看了上面的代码我们又会发现一些问题:
- 我们的迭代有点”傻“,我们要遍历字符串,随机抽取,随机生成,这个过程过于繁琐,直接影响效率。而且实际上我们是无法从已有的生成记录中再去进行“学习”的,它的遍历过程没有留下有效的结构信息。
- 我们控制不住它,即使是我们限制了迭代次数,在迭代范围内它也是过于随机了,导致生成的结果我们能插手的地方很少,我们没有办法以合适的粒度对其进行限制。而一不小心,它还经常生成长字符串。
对于第二个问题,我们还可以想办法进行改善,比如,我们限制标签的最大深度和最小深度,超过或者小于这个深度时,标签就不再出现,比如:
"<expr>":
[("<term> + <expr>", opts(min_depth=10)),
("<term> - <expr>", opts(max_depth=2)),
"<term>"]
但这样的解决方案能力有限,因为这样操作相当于我们人为限制了语法的“值域”,也就是说输出的结果范围被限制了,我们可能无法生成所需的fuzzing字符串。而且,我们永远没有探索最短、最长等特殊表达式的能力,比如1+1,这样的表达式你就只能等着它自己慢慢生成。
而对于第一个问题,因为我们使用简单的字符产组织,结构如此,永远没办法改善,只能另谋他路。
语法树
在算法问题中,我们常常一言不合就用树,因为树状结构简单清晰,还弥补了很多数据结构的缺点(虽然很多优点它也没继承),那么我们在这个问题上能不能使用树结构呢?我们简单思考:
- 有限状态机的结构与树非常契合,我们可以认为树的当前的节点就是一个状态,而这个状态的下一个状态,我们可以用该节点的子节点表示,有几个就挂几个子节点,可以一直继续下去。也就是说,节点的种类有限,节点的数量无限。同样用在我们的语法规则上也适用,我们生成的标签就可以作为节点,我们可以按照规则选择接下来的标签挂到节点上。
- 我们语法规则是马尔科夫链(当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态。但要注意,有限状态机本身不能算是马尔可夫链,因为实际上有限状态机的状态变换时一定的,没有概率一说,但我们生成字符串的规则却是带有随机性的)的一种特殊情况,它的每次状态变化都只依赖于当前状态,和之前的都没关系,所以对于树结构,我们只需要看当前的叶子节点即可,不需要关心前面节点的情况。
理论上的东西太抽象了,我们来看个例子,我们给出如下的语法规则(实际上就是四则运算规则):
我们按照上面的思路试试能不能建树:
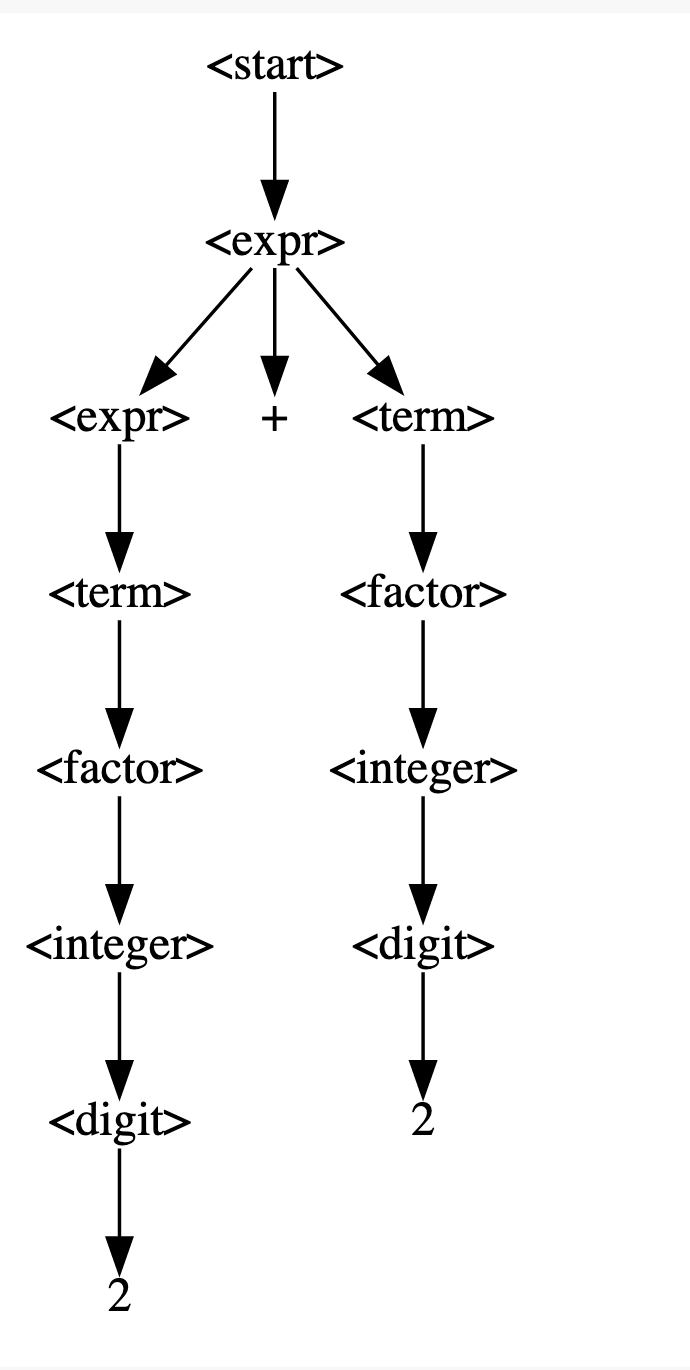
- start节点作为根节点
- start节点可以转移到expr节点,挂上expr节点
- expr节点有三个包,随机选一个挂上,比如expr + term包
- 现在我们有三个节点,其中,+不是非终端节点,它的使命已经完成,我们对其他两个节点重复操作
- 重复直到所有的叶子节点都是终端节点即可。
如此,我们得到了2+2这个数学表达式。这个东西我们管它叫派生树,也可以叫语法树。我们看看它解决上面的问题了吗?
- 时间上,我们遍历时不需要考虑整棵树,只需要检查叶子节点即可,效率大大提高
- 在控制方面,我们对于每一个叶子节点在遍历过程中都是可控的,我们可以人为在任何一步设置限定,不但不影响性能,编写程序也方便。
并且,我们可以看到,树结构还为我们提供了清晰的结构,让我们有了对于语法的“具体格式”,上面一章虽然也有结构信息保留下来,但结构信息杂乱,难以提取有效格式,而树结构天然就可供我们使用。我们可以进行大量的测试,我们手里有了大量树结构及其对应的代码覆盖等指标,我们完全可以选择其中优质的树结构进行相似度比较,从而提取更加优秀的树结构供我们使用。
比如bc人为限制不能输入+,如果我们按照普通的四则运算语法显然会导致大量的失效,但我们可以从有效的树中进行相似度比较,提取相似部分,这样我们就能慢慢去接近这套规则。因为树结构的存在,我们完全可以自由使用前面的知识,“养蛊”式的优化我们的树。
说完了理论,来简单看看代码实现,对于树结构,我们在python中有一套经典的保存方案:
derivation_tree = ("<start>",
[None])
即用二元组表示一棵树,其中,第一个表示节点,第二个是一个list,表示孩子。这套方案最大的问题是没法解决边的问题,但是我们现在对边也没什么讲究。
class GrammarFuzzer(GrammarFuzzer):
def choose_node_expansion(self, node, possible_children):
return random.randrange(0, len(possible_children))
def expand_node_randomly(self, node):
(symbol, children) = node
assert children is None
expansions = self.grammar[symbol]
possible_children = [self.expansion_to_children(
expansion) for expansion in expansions]
index = self.choose_node_expansion(node, possible_children)
chosen_children = possible_children[index]
chosen_children = self.process_chosen_children(chosen_children,
expansions[index])
return (symbol, chosen_children)
对于节点的扩充,其实和之前类似,都是先查语法,找到当前标签的包,随机选择一个,然后把包里所有的标签挂到节点上即可。到此,我们已经完全可以利用语法树来为我们生成fuzzing字符串了。
但是我们还不满意,我们说了树结构能帮助我们控制生成的过程,那应该怎么做呢?我们一般会定义如下的概念:
- 节点最小代价,即节点到终端节点需要消耗的最小“步数”,比如
<expr>→<term>→<factor>→<integer>→<digit>→ 1,expr走到终端节点最短路径如此,故其最小代价是5 - 节点最大代价,即节点到终端节点最大需要的步数,对于有递归的节点来说,就是无限大,对于digit来说,就是1
这两个概念可以帮助我们限制节点的走向,比如,我们可以规定,每一个节点都必须以最小的代价来进行生成(代码非常简单,我们检查节点所有可能的孩子的代价,对于包的情况,就是包内所有节点的代价的和,选择最小的挂上去即可),那么我们就会得到
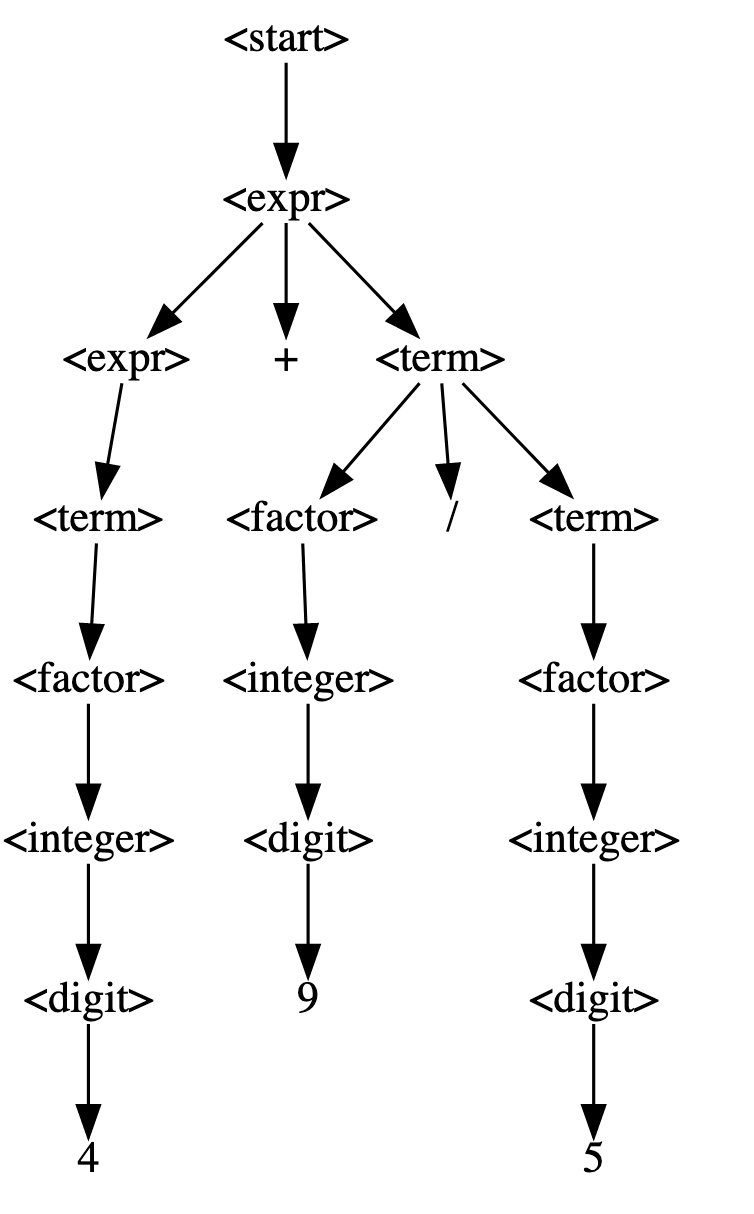
我们就得到了一棵相对简单的树,它的表达式长度也让人比较满意。我们同样也可以按照最大代价进行生成,我们限制递归次数即可,如此我们就可以得到较长的表达式。但是这些会导致“僵化”问题,即路径固定,比如如果我们的最短路径只有上面一条,导致我们一直走,那我们生成的格式就永远是x+y/z了
我们目前实际上有了三种节点策略:
- 最小代价生成,即找最小代价的,会造成“僵化”
- 最大代价生成,即找最大代价的,在递归较多的语法中,“僵化”可能性较小
- 随机找一个,不会“僵化”
实际使用中,我们可以对每个节点采取不同的策略,比如有的采取最小,有的采取随机,有的采取最大,然后再人为限制递归次数,我们就即可以保证生成字符串多种多样,得到较为理想的结果了。
总结
我们从没头没脑的随机生成fuzzing字符串到现在终于可以利用语法“随心所欲”的生成符合我们要求格式的字符串,但在语法方面,仍有大量的知识等着我们学习,下一篇内容仍将聚焦于语法部分,期待我们的史莱姆再次升级。











发表评论
您还未登录,请先登录。
登录